\(\left(x+y\right)^3=x^3+3x^2y+3xy^2-y^3\)
\(\left(x-y\right)^3=x^3-3x^2y+3xy^2-y^3\)
\(\left(2y-3\right)^3=8y^3-36y^2+54y-27\)
a: Ta có: \(\left(x+y\right)^3-\left(x-y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)
\(=6x^2y+2y^3\)
\(\left(x+y\right)^3=x^3+3x^2y+3xy^2-y^3\)
\(\left(x-y\right)^3=x^3-3x^2y+3xy^2-y^3\)
\(\left(2y-3\right)^3=8y^3-36y^2+54y-27\)
a: Ta có: \(\left(x+y\right)^3-\left(x-y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)
\(=6x^2y+2y^3\)
Sử dụng hằng đẳng thức khai triển và thu gọn biểu thức sau. A/. (x+y)^3-(x-y)^3
Sử dụng hằng đẳng thức khai triển và thu gọn biểu thức sau (1phần 3y+3)^3
Sử dụng hằng đẳng thức khai triển và thu gọn biểu thức sau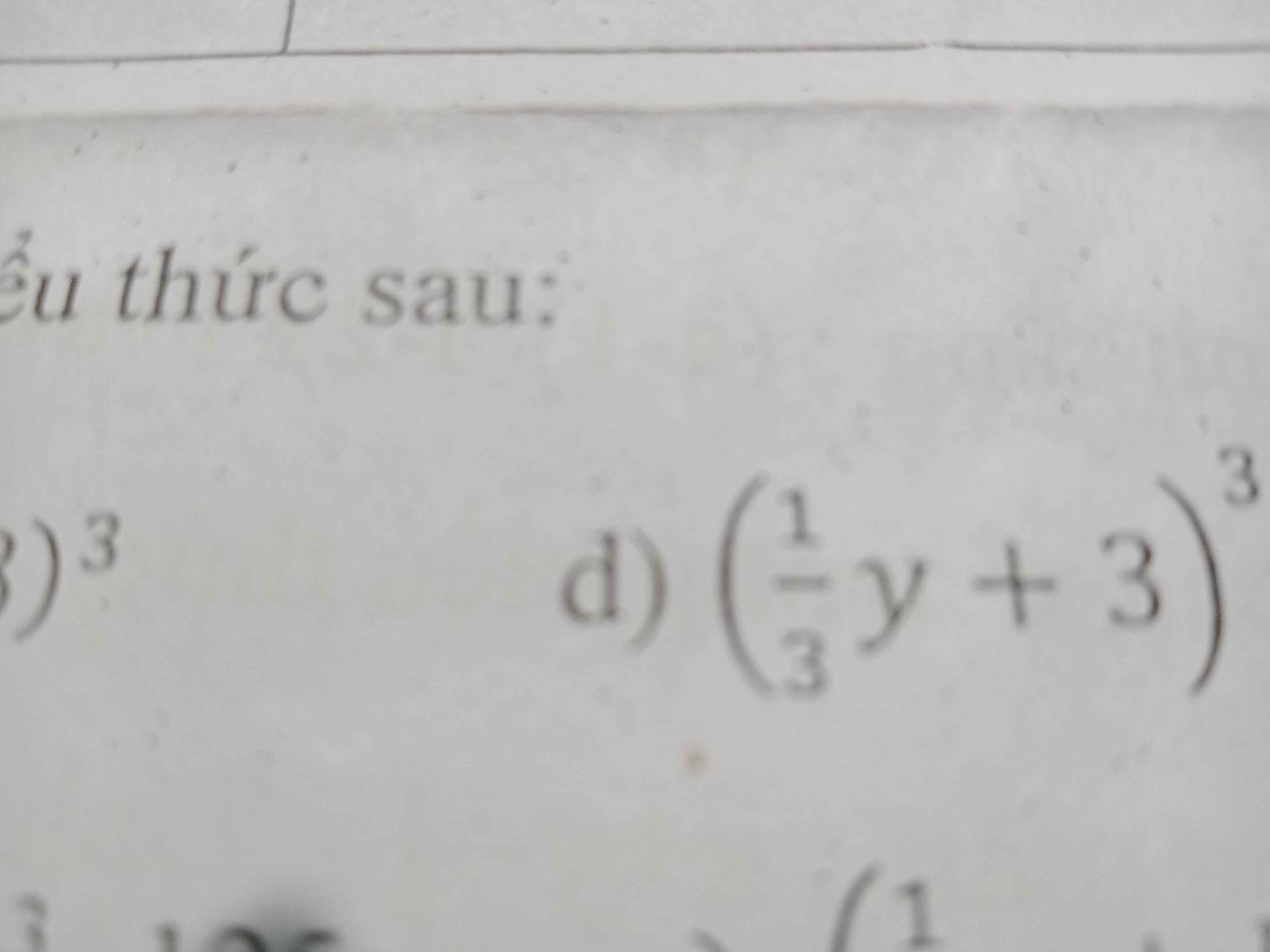
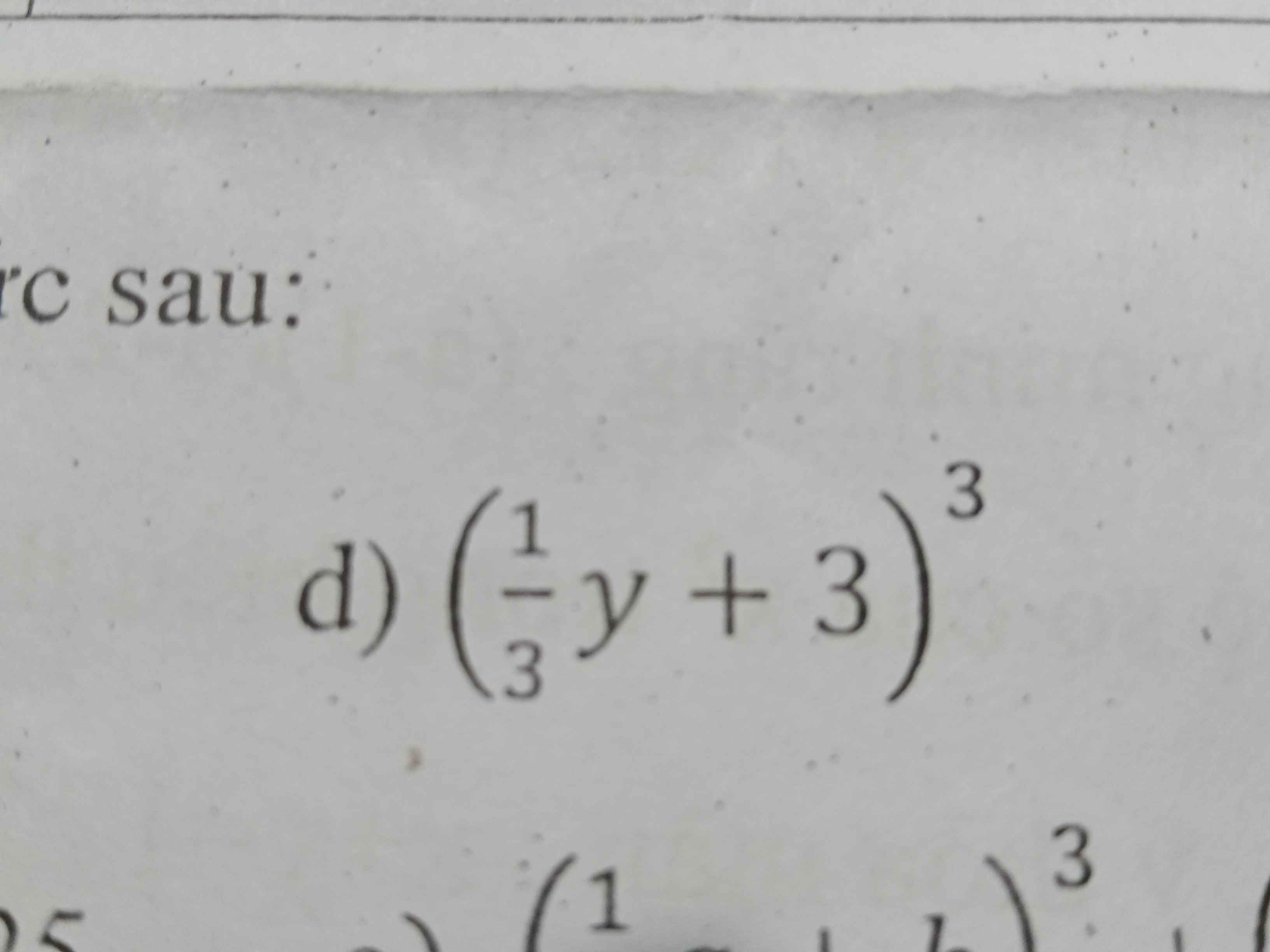
sử dụng các hằng đẳng thức đáng nhớ để khai triển các biểu thức (lớp 8 )
a/ (x + 2y)^3
b/ (2x - 1)^3
c/ (5x + 1) (5x + 1)
Dùng hằng đẳng thức để khai triển và thu gọn các biểu thức sau:
(a^3+ab+b^2)(a^2-ab+b^2)-(a^4+b^4)
Áp dụng hằng đẳng thức, khai triển các biểu thức sau:
a, \(\left(2x+y+3\right)^2\)
b, \(\left(x-2y+1\right)^2\)
c, \(\left(x^2-2xy^2-3\right)^2\)
Khai triển hằng đẳng thức
1)-(y+6)^2
2)-(4-y)^2
3)-(2/3+x)^2
4)-(x-3/2)^2
5)-(2+3y)^2
6)-(2y-3)^2
7)-(5x+2y)^2
8)-(2x-3/2)^2
Áp dụng hằng đẳng thức khai triển biểu thức sau:
a, \(\left(3x^2-2y^3\right)^2\)
b, \(\left(-2x^2-3\right)^2\)
a. Thực hiện phép nhân -\(\dfrac{3}{5}\) x^2y (x+3y^2)
b. Khai triển hằng đẳng thức: (x-√7y)^2