\(P=\dfrac{1}{1+2+3}+\dfrac{1}{1+2+3+4}+...+\dfrac{1}{1+2+3+...+59}\)
\(=\dfrac{1}{3\cdot\dfrac{4}{2}}+\dfrac{1}{4\cdot\dfrac{5}{2}}+...+\dfrac{1}{59\cdot\dfrac{60}{2}}\)
\(=\dfrac{2}{3\cdot4}+\dfrac{2}{4\cdot5}+...+\dfrac{2}{59\cdot60}\)
\(=2\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{59}-\dfrac{1}{60}\right)\)
\(=2\left(\dfrac{1}{3}-\dfrac{1}{60}\right)=2\cdot\dfrac{19}{60}=\dfrac{19}{30}< \dfrac{20}{30}=\dfrac{2}{3}\)
Đúng 2
Bình luận (0)

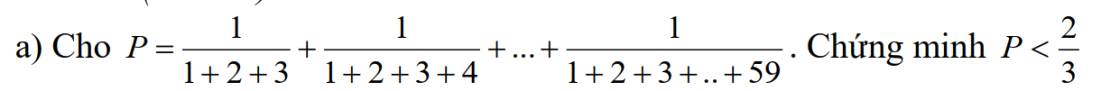




 sos giúp tớ với sos
sos giúp tớ với sos



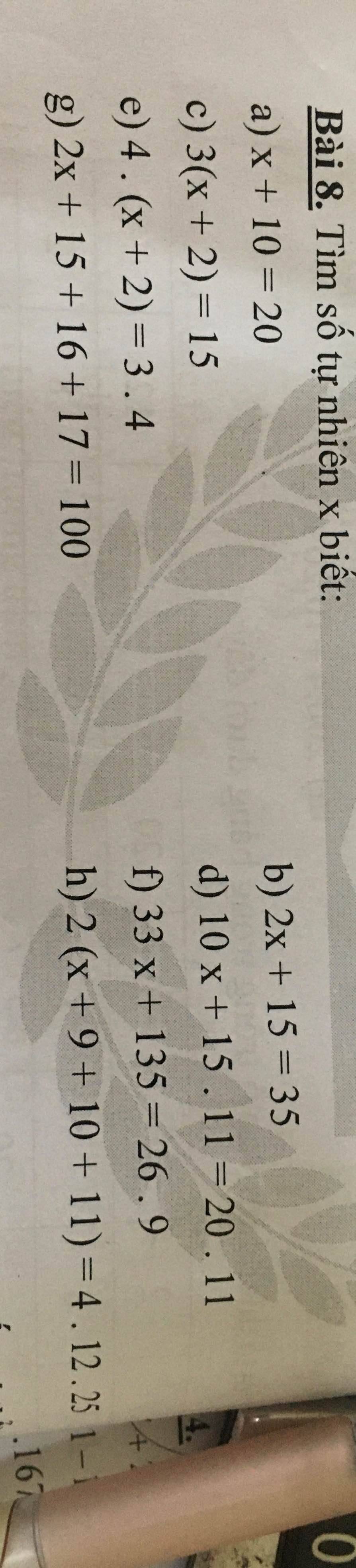




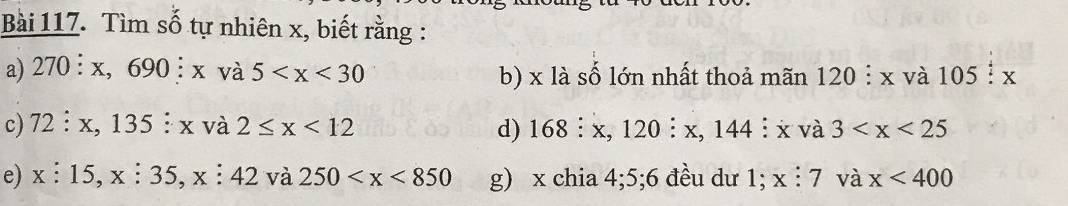


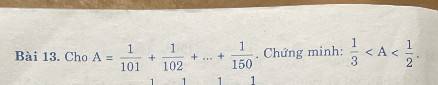 SOS
SOS 