Bài 117: Tìm số tự nhiên \(x\) biết rằng:
a, 270 \(⋮\) \(x\), 690 \(⋮\) \(x\) và 5 < \(x\) < 30
270 = 2.33.5; 690 = 2.3.5.23
ƯCLN(270; 690) = 2.3.5 = 30
270⋮\(x\); 690 \(⋮\) \(x\) ⇒ \(x\) \(\in\) ƯC(270; 690)
⇒ \(x\) \(\in\){ 1; 2; 3; 5; 6; 10; 15; 30}
Vì 5 < \(x\) < 30 nên \(x\) \(\in\) { 6; 10; 15}
117b, \(x\)max và 120 ⋮ \(x\); 105 ⋮ \(x\)
⇒ \(x\) là ước chung lớn nhất của 120 và 105
120 = 23.3.5; 105 = 3.5.7
ƯCLN (120; 105) = 3.5 = 15 ⇒ \(x\) = 15
72⋮ \(x\); 135 \(⋮\) \(x\) và 2 ≤ \(x\) < 12
72 ⋮ \(x\) ; 135 ⋮ \(x\) ⇒ \(x\) \(\in\) ƯC(72; 135)
72 = 23.32; 135 = 33.5
ƯCLN(72; 135) = 32 = 9
\(x\in\)Ư(9) = {1; 3; 9}
Vì 2 ≤ \(x\) < 12
vậy \(x\in\) {3; 9}
d, 168⋮\(x\); 120 ⋮ \(x\); 144 ⋮ \(x\) và 3 < \(x\) < 25
168⋮\(x;\) 120 ⋮ \(x\); 144 ⋮ \(x\)
\(x\) \(\in\) ƯC(168; 120; 144)
168 = 23.3.7; 120 = 23.3.5; 144 = 24.32
ƯCLN(168; 120; 144) = 23.3 = 24
\(x\) \(\in\) {1; 2; 3; 4; 6; 8; 12; 24}
vì 3 < \(x\) < 25 nên
\(x\) \(\in\) {4; 6; 8; 12; 24}
e, \(x\) ⋮ 15; \(x\) ⋮ 35; \(x\) ⋮ 42
⇒ \(x\) là BC(15; 35; 42)
15 = 3.5; 35 = 5.7; 47 = 6.7
BCNN(15; 35; 42) = 5.6.7 = 210
⇒ \(x\) \(\in\) {0; 210; 420; 630; 840; 1050;...;}
Vì 250 < \(x\) < 850
\(x\in\) {420; 630; 840}
g, \(x\) : 4; 5; 6 dư 1 ⇒ \(x\) - 1 ⋮ 4; 5; 6
4 = 22; 5 = 5; 6 = 2.3 ⇒ BCNN(4; 5; 6) = 22.5.3 = 60
⇒ \(x-1\) = 60.k ( k \(\in\)N*) ⇒ \(x\) = 60k + 1
⇒ 60k + 1 < 400 ⇒ k ≤ 6
\(x\) ⋮ 7 ⇒ 60k + 1 ⋮ 7 ⇒ 56k + 4k + 1 ⋮ 7
⇒ 4k + 1 ⋮ 7 ⇒ k \(\in\){\(\dfrac{3}{2}\); \(\dfrac{13}{4}\); 5 ; \(\dfrac{27}{4}\);...;}
Vì k \(\in\)N*; k ≤ 6 ⇒ k = 5
Thay k = 5 vào biểu thức \(x\) = 60k + 1 ta có: \(x\) = 60.5 + 1 = 301

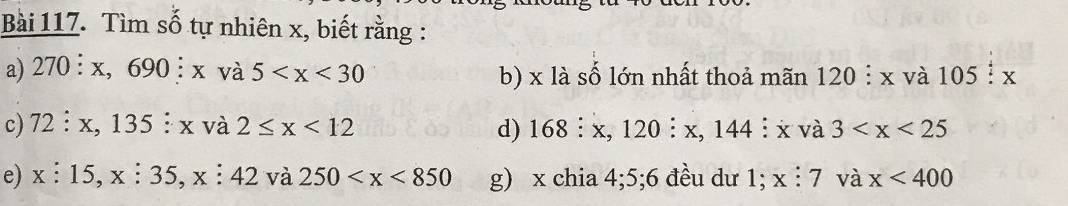



 sos giúp tớ với sos
sos giúp tớ với sos



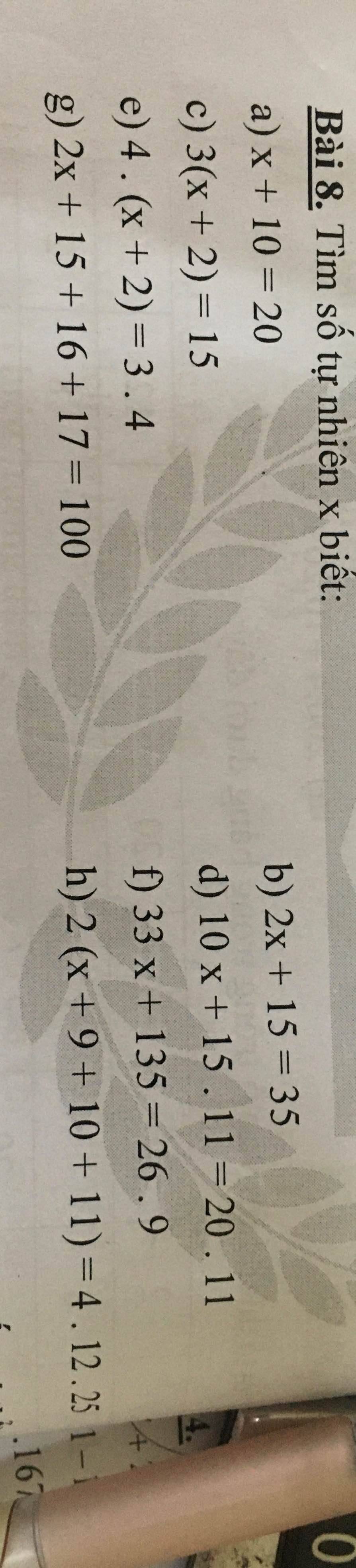






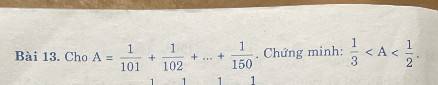 SOS
SOS