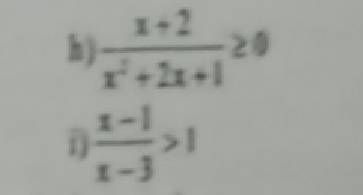h)\(\dfrac{x+2}{x^2+2x+1}\ge0\)
⇔\(\dfrac{x+2}{\left(x+1\right)^2}\ge0\)
⇔\(\dfrac{x+2}{\left(x+1\right)\left(x+1\right)}\ge\dfrac{0.\left(x+1\right)\left(x+1\right)}{\left(x+1\right)\left(x+1\right)}\)
⇒\(x+2\ge0\)
⇔\(x+2-2\ge0-2\)
⇔\(x\ge-2\)
i)\(\dfrac{x-1}{x-3}>1\)
⇔\(\dfrac{x-1}{x-3}>\dfrac{1.\left(x-3\right)}{1.x-3}\)
⇒\(x-1>x-3\)
⇔\(x-x>-3+1\)
⇔\(0x>-2\)
Đúng 3
Bình luận (0)