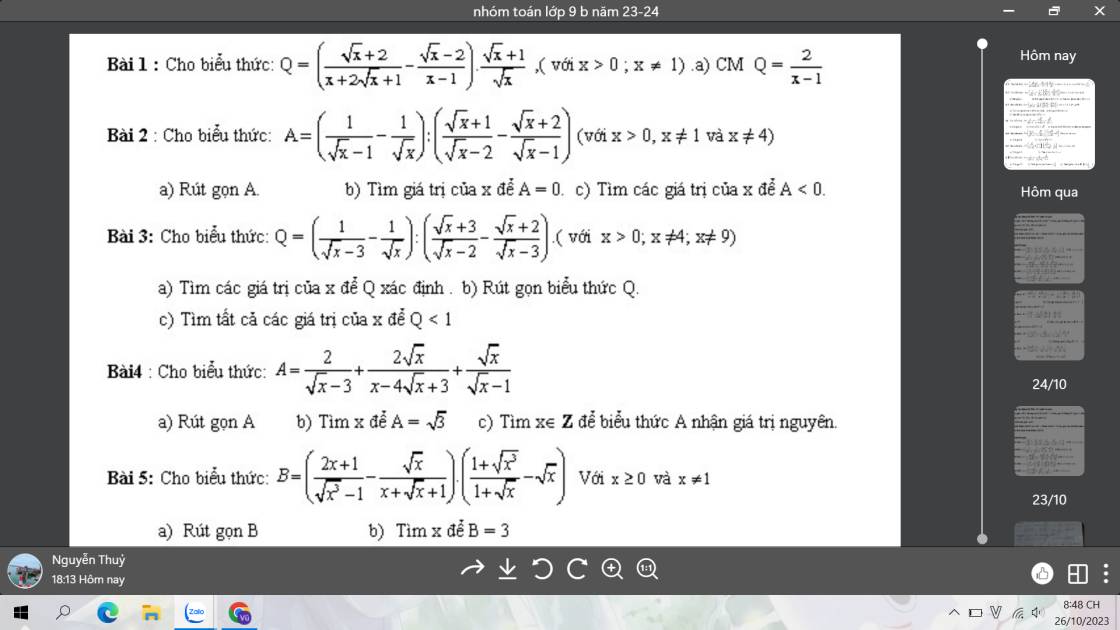
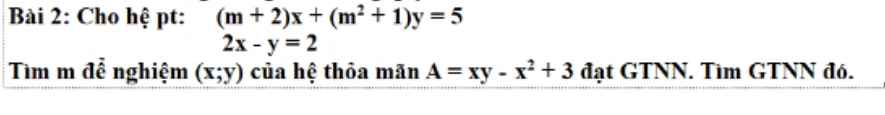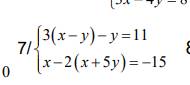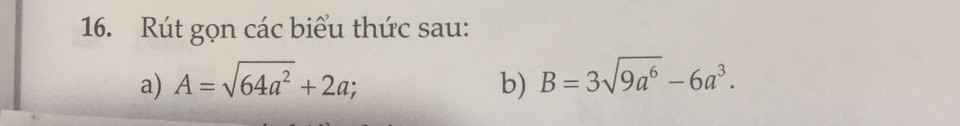Đề yêu cầu rút gọn hả bạn?
\(P=\left(\dfrac{x-\sqrt{x}+2}{x-\sqrt{x}-2}-\dfrac{x}{x-2\sqrt{x}}\right):\dfrac{1-\sqrt{x}}{2-\sqrt{x}}\) (ĐKXĐ: \(x>0;x\ne4;x\ne1\))
\(=\left[\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}-\dfrac{x}{\sqrt{x}\left(\sqrt{x}-2\right)}\right]\cdot\dfrac{2-\sqrt{x}}{1-\sqrt{x}}\)
\(=\left[\dfrac{x-\sqrt{x}+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}\right]\cdot\dfrac{2-\sqrt{x}}{1-\sqrt{x}}\)
\(=\dfrac{x-\sqrt{x}+2-x-\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}-1}\)
\(=\dfrac{-2\sqrt{x}+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{-2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}=\dfrac{-2}{\sqrt{x}+1}\)
$\text{#}Toru$

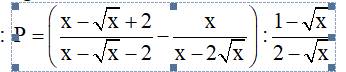 sos mn ơi
sos mn ơi