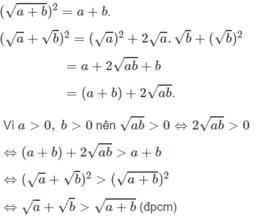Các câu hỏi tương tự
a) So sánh ...
a
)
25
+
9
v
à
25
+
9
b
)
v
ớ
i
a
0
;
b
0
;
c
h
ứ
n
g
m
i
n
h
a...
Đọc tiếp
a) So sánh ...
a ) 25 + 9 v à 25 + 9 b ) v ớ i a > 0 ; b > 0 ; c h ứ n g m i n h a + b < a + b
a) So sánh .. 25 - 16 v à 25 - 16
b) Chứng minh rằng với a>b>0 thì
... a - b < a - b
a) so sánh \(\sqrt{36-25}và\sqrt{36}-\sqrt{25}\)
b) chứng minh với a>0, b>0 thì \(\sqrt{a}-\sqrt{b}< \sqrt{a-b}\)
Với a ≥ 0 và b ≥ 0, chứng minh a + b 2 ≥ a + b 2
Chứng minh các đẳng thức sau:
a
+
b
b
2
a
2
b
4
a
2
+
2
a
b
+...
Đọc tiếp
Chứng minh các đẳng thức sau: a + b b 2 a 2 b 4 a 2 + 2 a b + b 2 = a v ớ i a + b > 0 v à b ≠ 0
Chứng minh các đẳng thức sau:
a
)
1
−
a
a
1
−
a
+
a
1
−
a
1
−...
Đọc tiếp
Chứng minh các đẳng thức sau:
a ) 1 − a a 1 − a + a 1 − a 1 − a 2 = 1 v ớ i a ≥ 0 v à a ≠ 1 b ) a + b b 2 a 2 b 4 a 2 + 2 a b + b 2 = | a | v ó i a + b > 0 v à b ≠ 0
với a>0 và b>0, chứng minh \(\sqrt{a+b}< \sqrt{a}+\sqrt{b}\)
giúp mình với
bài 5: a) so sánh \(\sqrt{25}+\sqrt{9}\) và \(\sqrt{25+9}\)
b)CMR: a>0,b>0 thì \(\sqrt{a+b}\)<\(\sqrt{a}+\sqrt{b}\)
a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy: ![]()
b) Cho a, b, c > 0. Chứng minh rằng: ![]()
c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab