\(3>\sqrt{3}+1;1< \sqrt{5}-1;2\sqrt{29}>10\)
\(2\sqrt{3}>3\sqrt{2};\sqrt{175}>3\sqrt{19};3+\sqrt{15}< 7\)
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
so sánh các số sau: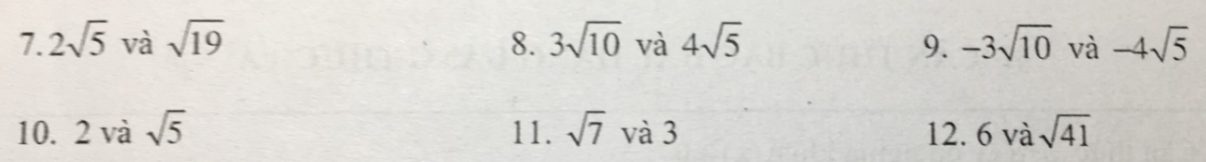
So sánh các số sau: \(\dfrac{1}{\sqrt{7}}+\dfrac{1}{\sqrt{11}}\) và \(\dfrac{2}{3}\)
Bài 1. Tính căn bậc hai số học của các số sau:
1) 36
2) 81
3) 121
4) 144
5) 0,16
7) 29
8) 0
Bài 2. So sánh các căn bậc hai sau:
1) 6 và 41
2) 19 và 4
3) 21 và 5
4) 7 và 51
Giải các phương trình sau bằng cách (chuyển các số hạng tự do sang vế phải bằng công thức nghiệm) và so sánh kết quả tìm được: 4 x 2 - 9 = 0
Giải các phương trình sau bằng cách (chuyển các số hạng tự do sang vế phải bằng công thức nghiệm) và so sánh kết quả tìm được: 5 x 2 + 20 = 0
Giải các phương trình sau bằng cách (chuyển các số hạng tự do sang vế phải bằng công thức nghiệm) và so sánh kết quả tìm được: 3 x 2 - 12 + 145 = 0
Giải các phương trình sau bằng cách (chuyển các số hạng tự do sang vế phải bằng công thức nghiệm) và so sánh kết quả tìm được: 2 x 2 - 2 + 3 = 0
so sánh các số sau
\(\sqrt{3}\) và \(5-\sqrt{8}\)
So sánh các số thực sau : \(\frac{23-2\sqrt{19}}{3}\)và \(\sqrt{27}\)