+) Với a < 0
Ta có: 2 < 3
=> 2a > 3a (Nhân a vào 2 vế của BĐT)
+) Với a = 0
=> 2a = 3a (2.0 = 3.0 = 0)
+) Với a > 0
Ta có: 2 < 3
=> 2a < 3a (Nhân a vào 2 vế của BĐT).
+) Với a < 0
Ta có: 2 < 3
=> 2a > 3a (Nhân a vào 2 vế của BĐT)
+) Với a = 0
=> 2a = 3a (2.0 = 3.0 = 0)
+) Với a > 0
Ta có: 2 < 3
=> 2a < 3a (Nhân a vào 2 vế của BĐT).
Cho ∫ 0 2 2 x ln 1 + x d x = a ln b với a , b ∈ N * và b là số nguyên tố. Tính 3 a + 4 b .
A. 42
B. 2
C. 12
D. 32
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có A B = 3 a , A D = 3 a , A A ' = 2 a . Góc giữa đường thẳng AC’ với mặt phẳng (ABC) bằng
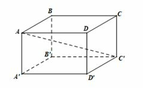
A. 60
B. 45
C. 120
D. 30
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, AD=2a, SA=3a và SA vuông góc với mặt đáy. Góc giữa đường thẳng SD và mặt phẳng (ABCD) là:
A. S A D ^ .
B. A S D ^ .
C. S D A ^ .
Biết ∫ 0 π 2 cos x sin 2 x + 3 sin x + 2 d x = a ln 2 + b ln 3 với a, b. c là số nguyên. Tính P = 2a + b.
A. 3
B. 7
C. 5
D. 1
Cho hàm số y=f(x) có đạo hàm y ' = x 2 - 12 x + 1 4 ( b + 3 a ) ∀ x ∈ R , biết hàm số luôn có hai cực với a, b là các số thực không âm thỏa mãn 3 b - a ≤ 6 . Tìm giá trị lớn nhất của biểu thức P = 2a+b
A. 1
B. 9
C. 8
D. 6
Cho ∫ − 1 4 x ln x + 2 d x = a ln 6 + 5 b với a, b là các số nguyên dương. Giá trị 2 a + 3 b bằng
A. 24.
B. 26.
C. 27.
D. 23.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với A B = 3 a ; B C = a , cạnh bên S D = 2 a và SD vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng
A. 3 a 3
B. a 3
C. 2 a 3
D. 6 a 3
Cho hình chóp S.ABCD có đáy là hình chữ nhật với A B = 2 a , A D = 3 a . Cạnh bên SA vuông góc với đáy ( A B C D ) v à S A = a . Tính thể tích V của khối chóp S.ABCD.
A. V = 6 a 3
B. V = a 3
C. V = 3 a 3
D. V = 2 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với A B = 3 a , B C = a , cạnh bên S D = 2 a và SD vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng
A. 3 a 3
B. a 3
C. 2 a 3
C. 6 a 3