Đáp án D
Hình chóp tam giác đều có 3 mặt phẳng đối xứng đó là các mặt phẳng đi qua cạnh bên và trung điểm cạnh đối diện
Đáp án D
Hình chóp tam giác đều có 3 mặt phẳng đối xứng đó là các mặt phẳng đi qua cạnh bên và trung điểm cạnh đối diện
Cho hình chóp tam giác đều S.ABC có đáy ABC là tam giác đều cạnh a, cạnh SA = 2 a 3 3 . Gọi D là điểm đối xứng của B qua C. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.A
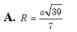
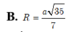
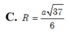
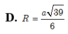
Cho hình chóp đều S.ABC, đáy ABC cạnh a, S A = 2 a 3 3 . Gọi D là điểm đối xứng với B qua C. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABD
A. R = a
B. R = a 2 2
C. R = a 37 6
D. R = a 35 6
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng đáy. Biết góc B A C ^ = 30 0 , S A = a và B A = B C = a . Gọi D là điểm đối xứng với B qua AC. Khoảng cách từ B đến mặt (SCD) bằng
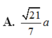
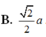
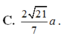
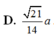
Tính thể tích V của hình chóp S.ABC có đáy là tam giác đều có cạnh bằng a, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBC) bằng 3 a/4. Thể tích của hình chóp S.ABC là:
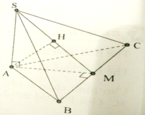
A. V = 3 8 a 3
B. V = 2 12 a 3
C. V = 3 12 a 3
D. V = 3 24 a 3
Gọi n là số mặt phẳng đối xứng của hình chóp tứ giác đều. Tìm n.
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. Biết ΔSAB là tam giác đều và thuộc mặt phẳng vuông góc với mặt phẳng (ABC). Tính thể tích khối chóp S.ABC biết AB = a, AC = a 3 .
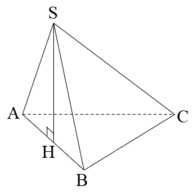
A. a 3 6 12
B. a 3 6 4
C. a 3 2 6
D. a 3 4
Cho hình chóp S . A B C có đáy A B C là tam giác đều cạnh bằng 1. Biết khoảng cách từ A đến mặt phẳng S B C là 6 4 , từ B đến mặt phẳng S A C là 15 10 ; từ C đến mặt phẳng S A B là 30 20 và hình chiếu vuông góc của S xuống đáy nằm trong tam giác A B C . Thể tích khối chóp S . A B C bằng
A. 1 36
B. 1 48
C. 1 12
D. 1 24
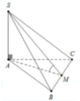
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng đáy, tam giác SBC đều cạnh a, góc giữa mặt phẳng (SBC) và mặt phẳng đáy là 30º. Tính thể tích V của khối chóp S.ABC
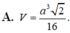
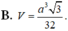
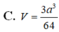
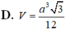
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng đáy, tam giác SBC đều cạnh a, góc giữa mặt phẳng (SBC) và mặt phẳng đáy là 30 o Tính thể tích V của khối chóp S.ABC
A. V = a 3 2 16
B. V = a 3 3 32
C. V = 3 a 3 64
D. V = a 3 3 12