\(A=\dfrac{\left(2^2\cdot3\right)^6+8^4\cdot3^5}{2^{12}\cdot3^5-4^6\cdot9^2}-\dfrac{4\cdot\left(125\cdot7\right)^3+5^9\cdot14^3}{125^3\cdot49^2-5^9\cdot7^3}\)
\(=\dfrac{2^{12}\cdot3^6+2^{12}\cdot3^5}{2^{12}\cdot3^5-2^{12}\cdot3^4}-\dfrac{2^2\cdot5^9\cdot7^3+5^9\cdot7^3\cdot2^3}{5^9\cdot7^4-5^9\cdot7^3}\)
\(=\dfrac{2^{12}\cdot3^5\left(3+1\right)}{2^{12}\cdot3^4\left(3-1\right)}-\dfrac{2^2\cdot5^9\cdot7^3\left(1+2\right)}{5^9\cdot7^3\left(7-1\right)}\)
\(=\dfrac{3\cdot4}{2}-\dfrac{4\cdot3}{6}=6-2=4\)
Đúng 3
Bình luận (0)
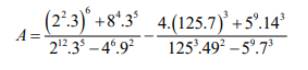
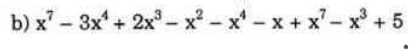Rút Gọn 
