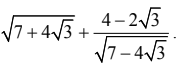Lời giải:
Đặt $\sqrt{\sqrt{3}-1}=a$ thì $\sqrt{3}-1=a^2$
$\sqrt{3}+1=\frac{2}{a^2}$
\(A=(\sqrt{\frac{(a^2+1)^2}{2}+\frac{3}{2}-2a}+\frac{a^2}{\sqrt{2}})a\)
\(=\sqrt{\frac{a^4+2a^2}{2}+2-2a}+\frac{a^2}{\sqrt{2}})a=(\sqrt{\frac{1}{2}a^4+a^2+(\frac{2}{a^2}-a^2)-2a}+\frac{a^2}{\sqrt{2}})a\)
\(=(\sqrt{\frac{1}{2}a^4+\frac{2}{a^2}-2a}+\frac{a^2}{\sqrt{2}})a\)
\(=(\sqrt{(\frac{a^2}{\sqrt{2}}-\sqrt{\frac{2}{a^2}})^2}+\frac{a^2}{\sqrt{2}})a\)
\(=(|\frac{a^2}{\sqrt{2}}-\frac{\sqrt{2}}{a}|+\frac{a^2}{\sqrt{2}})a\)
\(=(|\frac{\sqrt{3}-1}{\sqrt{2}}-\frac{\sqrt{2}}{\sqrt{\sqrt{3}-1}}|+\frac{\sqrt{3}-1}{\sqrt{2}}).\sqrt{\sqrt{3}-1}\)
\(=(\frac{\sqrt{2}}{\sqrt{\sqrt{3}-1}}-\frac{\sqrt{3}-1}{\sqrt{2}}+\frac{\sqrt{3}-1}{\sqrt{2}}).\sqrt{\sqrt{3}-1}=\frac{\sqrt{2}}{\sqrt{\sqrt{3}-1}}.\sqrt{\sqrt{3}-1}=\sqrt{2}\)