Chọn C.
Ta có A = sin 2a.tan2a + 4sin2a - tan2a + 3cos2a
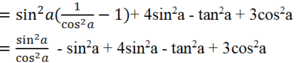
= 3sin2a + 3cos2a = 3.
Chọn C.
Ta có A = sin 2a.tan2a + 4sin2a - tan2a + 3cos2a
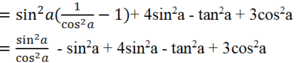
= 3sin2a + 3cos2a = 3.
Rút gọn biểu thức: \(A=sin\left(a+b\right)+sin\left(\frac{\pi}{2}-a\right)sin\left(-b\right)\)
Rút gọn biểu thức A= sin x + sin 2 x + sin 3 x cos x + cos 2 x + cos 3 x
A. tan4x
B. tan 3x
C. tan 2x
D. tan x + tan 2x
Rút gọn biểu thức : A = sin( a - 160) .cos( a + 140) – sin( a + 140) .cos(a - 160), ta được :
A. cos2a
B. sin a
C. -0,5
D. 0
rút gọn biểu thức P= sin(π/2-alpha)+cos(alpha+5π) a0 b 2cos alpha c 2 sin alpha d1
Kết quả rút gọn của biểu thức sin a + tan a c o s a + 1 2 + 1 bằng
A. cos2a
B. tan2a
C. 1 cos 2 a
D. 1 sin 2 a
Biểu thức A = cos 750 o + sin 420 o sin - 330 o - cos - 390 o có giá trị rút gọn bằng
A. - 3 - 3
B. 2 - 3 3
C. 2 3 3 - 1
D.Tất cả sai
Biểu thức A = sin 515 o . cos - 475 o + c o t 222 o . c o t 408 o c o t 415 o . c o t ( - 505 o ) + tan 197 o . tan 73 o có kết quả rút gọn bằng
![]()
![]()
![]()
![]()
Cho 0 < α < π/2. Biểu thức S = sin 4 α - 2 sin 2 α sin 4 α + 2 sin 2 α có thể rút gọn thành biểu thức nào sau đây?
A. - tan 2 α B. tanα
C. c o t 2 α D. cotα
1.\(\)chứng minh hệ thức: \(\dfrac{sin\alpha+sin3\alpha+sin5\alpha}{cos\alpha+cos3\alpha+cos5\alpha}=tan3\alpha\)
2.rút gọn biểu thức: \(\dfrac{1+sin4\alpha-cos4\alpha}{1+cos4\alpha+sin4\alpha}\)
3. Tính \(96\sqrt{3}sin\dfrac{\pi}{48}cos\dfrac{\pi}{48}cos\dfrac{\pi}{24}cos\dfrac{\pi}{12}cos\dfrac{\pi}{6}\)
4. chứng minh rằng trong một △ABC ta có:
tanA + tanB + tanC = tanA tanB tanC (A,B,C cùng khác \(\dfrac{\pi}{2}\))