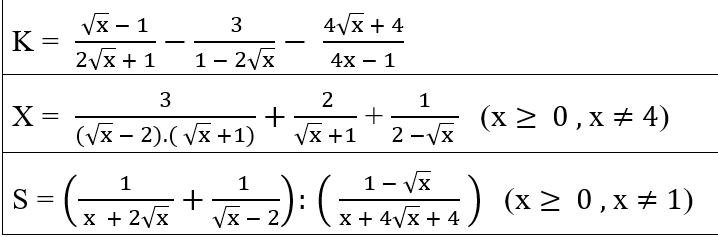\(B=\dfrac{x}{x-\sqrt{x}}+\dfrac{2}{x+2\sqrt{x}}+\dfrac{x+2}{x\sqrt{x}+x-2\sqrt{x}}\)
\(=\dfrac{\sqrt{x}\cdot\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{2}{\sqrt{x}\left(\sqrt{x}+2\right)}+\dfrac{x+2}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x\left(\sqrt{x}+2\right)+2\left(\sqrt{x}-1\right)+x+2}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x\sqrt{x}+3x+2\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}\left(x+3\sqrt{x}+2\right)}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+3\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)

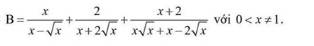






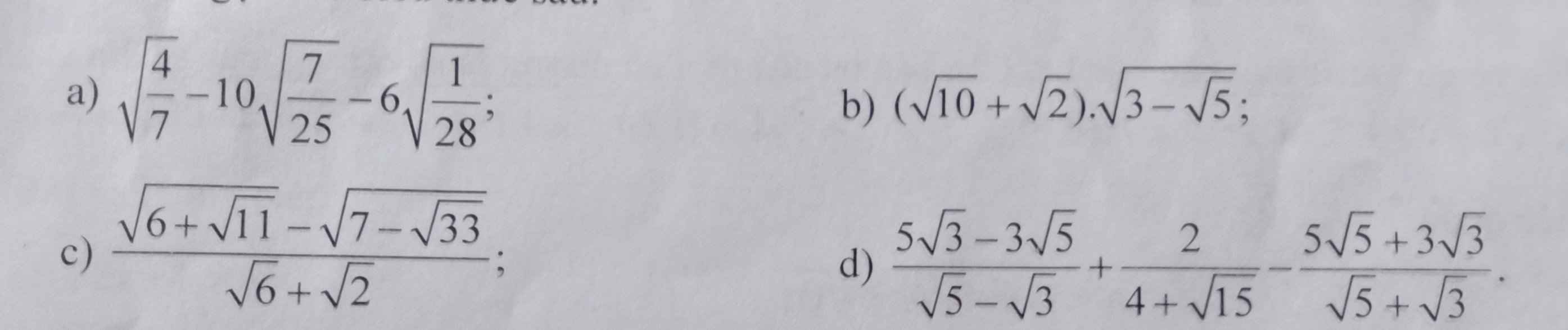 rút gọn giúp mình vs ạ
rút gọn giúp mình vs ạ 
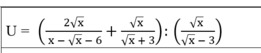

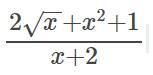 Rút gọn giúp mình với ạ
Rút gọn giúp mình với ạ




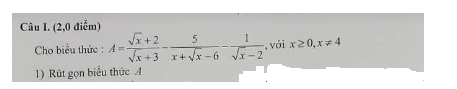 rút gọn biểu thức, giúp e với ạ :<
rút gọn biểu thức, giúp e với ạ :<