Ta có:
x 3 + 6 x 2 + 12 x + 8 = x 3 + 3 x 2 . 2 + 3 . x . 2 2 + 2 3 = x + 2 3
x 2 + 4 x + 4 = x + 2 2 ; 2 x + 4 = 2 x + 2
Mẫu thức chung: 2 x + 2 3
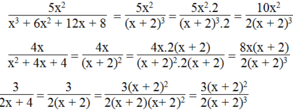
Ta có:
x 3 + 6 x 2 + 12 x + 8 = x 3 + 3 x 2 . 2 + 3 . x . 2 2 + 2 3 = x + 2 3
x 2 + 4 x + 4 = x + 2 2 ; 2 x + 4 = 2 x + 2
Mẫu thức chung: 2 x + 2 3
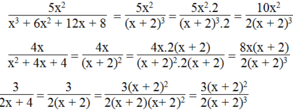
Quy đồng mẫu thức các phân thức sau
3x / x + 1 và x + 4/ x + 2
5 / x^2 + x và 6 / x^2 - 1
4 / x^2 - 5x - 4 và x + 1/ 2x^2 - 8x
x + 3 / 2x^2 - 15x - 8 và 3 / x^2 - 8x
giải giùm nha
quy đồng mẫu hai phân thức (a-x)/(6*x^2-a*x-2*a^2) và (a+x)/(3*x^2+4*a*x-4*a^2)
quy đồng mẫu thức của các phân thức
\(\dfrac{1}{x+2};\dfrac{-3x}{x-2};\dfrac{3}{x^2-4x+4}\)
\(\dfrac{-1}{2x+2};\dfrac{3}{2-2x};\dfrac{5}{4x^2+4x+1}\)
Quy đồng mẫu các phân thức sau:
a)\(\dfrac{x}{x-y}\); \(\dfrac{y}{\left(x-y\right)^2}\) ; \(\dfrac{1}{\left(y-x\right)^3}\)
b) \(\dfrac{1}{2x+4};\dfrac{x}{2x-4};\dfrac{3}{4-x^2}\)
Quy đồng mẫu các phân thức sau:
a)\(\dfrac{x}{x-y};\dfrac{y}{\left(x-y\right)^2};\dfrac{1}{\left(y-x\right)^3}\)
b) \(\dfrac{1}{2x+4};\dfrac{x}{2x-4};\dfrac{3}{4-x^2}\)
Quy đồng mẫu thức hai phân thức
4 phần x+2 và 2-x phần 3(x bình +4x+4)
Quy đồng mẫu các phân thức:
1) 7x-1/2x^2+6x; 3-2x/x^2-9
2) 2x-1/x-x^2; x+1/2-4x+2x^2
3) x-1/x^3+1; 2x/x^2-x+1; 2/x+1
4) 7/5x; 4/x-2y; x-y/8y^2-2x^2
5) x/x^3-1; x+1/x^2-x; x-1/x^2+x+1
6) x/x^2-2ax+a^2; x+a/x^2-ax
Cho các phân thức x − 3 2 x 2 − 3 x − 2 và 2 x − 1 x 2 + x − 6 với x ≠ − 3 ; x ≠ − 1 2 và x ≠ 2 . Không dùng cách phân tích các mẫu thức thành nhân tử, hãy chứng tỏ rằng có thể quy đồng mẫu thức hai phân thức này với mẫu thức chung là N = 2 x 3 + 3 x 2 − 11 x − 6 .
Phân tích đa thức thành nhân tử:
x^4+x^3+6.x^2+5.x+5
x^4-2.x^3-12.x^2+12.x+36
X^8.y^8+x^4.y^4+1
quy đồng mẫu thức của các phân thức sau
\(x^2+1,\frac{x^4}{x^{2-1}}\)
\(\frac{x^3}{x^3-3x^2y+3xy^2-y^3},\frac{x}{y^2-xy}\)