Các câu hỏi tương tự
qua mỗi đỉnh của tam giác kẻ đường song song với cạnh đối diện với nó a ) chứng minh rằng mỗi đường thẳng cắt hai đường thẳng còn lại b ) chứng minh rằng ba giao điểm là ba đỉnh của một tam giác .
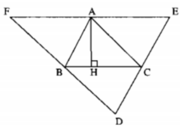
Cho tam giác ABC. Qua mỗi đỉnh A, B, C kẻ các đường thẳng song song với cạnh đối diện, chúng cắt nhau tạo thành tam giác DEF (hình dưới). Chứng minh rằng A là trung điểm của EF.
Bài toán1: Qua mỗi đỉnh của tam giác kẻ đường thẳng song song với cạnh đối diện của nó:a) Chứng minh rằng: Mỗi đường thẳng cắt 2 đường thẳng còn lại.b)Chúng minh rằng:Qua giao điểm là 3 đỉnh của 1 tam giác.Bài toán 2:Cho tam giá ABC có AB bé thua AC.Hãy nói cách xác định M thuộc AC sao cho AM+MBAC.Bài toán 3: Cho biết 2 đường trung trực của 2 đoạn thẳng AC và CD cắt nhau tại O.Trong các mệnh đề sau , mênh đề nào đúng mệnh đề nào sai:a) 2 đường thẳng AB và CD song song với nhau.b) 2 đường thẳng A...
Đọc tiếp
Bài toán1: Qua mỗi đỉnh của tam giác kẻ đường thẳng song song với cạnh đối diện của nó:
a) Chứng minh rằng: Mỗi đường thẳng cắt 2 đường thẳng còn lại.
b)Chúng minh rằng:Qua giao điểm là 3 đỉnh của 1 tam giác.
Bài toán 2:Cho tam giá ABC có AB bé thua AC.Hãy nói cách xác định M thuộc AC sao cho AM+MB=AC.
Bài toán 3: Cho biết 2 đường trung trực của 2 đoạn thẳng AC và CD cắt nhau tại O.Trong các mệnh đề sau , mênh đề nào đúng mệnh đề nào sai:
a) 2 đường thẳng AB và CD song song với nhau.
b) 2 đường thẳng AB và CD cắt nhau.
c) Điểm O cắt đường thẳng cách đều 4 điểm A,B,C,D.
Các bạn giúp mik giải 3 bài toán hình này nhé! Sáng mai mik phải nộp rồi!
Cho tam giác ABC. Qua mỗi đỉnh A, B, C kẻ các đường thẳng song song với cạnh đối diện, chúng cắt nhau tạo thành tam giác DEF
a. Chứng minh rằng A là trung điểm của EF.
b. Các đường cao của tam giác ABC là các đường trung trực của tam giác nào?
CHo Tam giác ABC , qua mỗi đỉnh A,B,C kẻ các đường song song với cạnh đối diện . Chúng cắt nhau tạo thành tam giác DEF
Chứng minh rằng các đường cao của tam giác ABC là đường trung trực của tam giác DEF
Cho tam giác ABC, qua đỉnh A kẻ đường thẳng a song song với BC, qua đỉnh B kẻ đường thẳng b song song với cạnh AC
a) Vẽ được mấy đường thẳng a, mấy đường thẳng b ? Vì sao?
b) Chứng minh rằng a và b cắt nhau
Cho tam giác vuông tại A (ABAC) . Kẻ AH vuông góc ( H thuộc BC).Lấy điểm D thuộc tia đối của tia HA sao cho HDHA a) Chứng minh rằng tam giác CAH tam giác CDH và tia CB là tia phân giác của ACD b) Qua D kẻ một đường thẳng song song với AC cắt BC ở M. Chứng minh rằng tam giác CAH tam giác MDH và AD là đường trung trực của đoạn CM c) Kẻ BN vuông góc với đường thẳng AM ( N thuộc tia AM ) . Chứng minh rằng ba điểm B , N , D thẳng hàng.
Đọc tiếp
Cho tam giác vuông tại A (AB>AC) . Kẻ AH vuông góc ( H thuộc BC).Lấy điểm D thuộc tia đối của tia HA sao cho HD=HA a) Chứng minh rằng tam giác CAH= tam giác CDH và tia CB là tia phân giác của ACD b) Qua D kẻ một đường thẳng song song với AC cắt BC ở M. Chứng minh rằng tam giác CAH= tam giác MDH và AD là đường trung trực của đoạn CM c) Kẻ BN vuông góc với đường thẳng AM ( N thuộc tia AM ) . Chứng minh rằng ba điểm B , N , D thẳng hàng.
Cho tam giác ABC với trung tuyến AD. Qua D kẻ đường thẳng song song với AB; qua B kẻ đường thẳng song song với AD. Hai đường thẳng trên cắt nhau tại E. Gọi K là trung điểm của đoạn EC. Chứng minh rằng: Ba điểm A, D, K thẳng hàng.
Cho Tam giác ABC, qua mỗi đỉnh A,B,C vẽ các đường song song với cạnh đối diện, các đường này cắt nhau tạo thành tam giác DEF.
a, Chứng minh CF,AD,BE đồng quy.
b, Chứng minh 3 đường cao của tam giác ABC là 3 đường trung trực của tam giác DEF.










