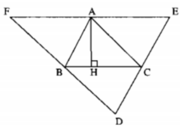
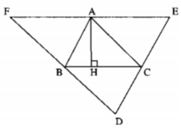
Xét ΔABC và ΔCEA, ta có:
∠(ACB) = ∠(CAE) (so le trong, AE // BC)
AC cạnh chung
∠(CAB) = ∠(ACE) (so le trong, CE // AB)
Suy ra: ΔABC = ΔCEA (g.c.g)
⇒ BC = AE (1)
Xét ΔABC và ΔBAF, ta có:
∠(ABC) = ∠(BAF) (so le trong, AF // BC)
AB cạnh chung
∠(BAC) = ∠(ABF) (so le trong, BF // AC)
Suy ra: ΔABC = ΔBAF (g.c.g)
⇒ AF = BC (2)
Từ (1) và (2) suy ra: AE = AF
Vậy A là trung điểm của EF.
Cho tam giác ABC. Qua mỗi đỉnh A, B, C kẻ các đường thẳng song song với cạnh đối diện, chúng cắt nhau tạo thành tam giác DEF
a. Chứng minh rằng A là trung điểm của EF.
b. Các đường cao của tam giác ABC là các đường trung trực của tam giác nào?
Cho tam giác ABC. Qua mỗi đỉnh A, B, C kẻ các đường thẳng song song với cạnh đối diện, chúng cắt nhau tạo thành tam giác DEF (hình dưới). Các đường cao của tam giác ABC là các đường trung trực của tam giác nào?
CHo Tam giác ABC , qua mỗi đỉnh A,B,C kẻ các đường song song với cạnh đối diện . Chúng cắt nhau tạo thành tam giác DEF
Chứng minh rằng các đường cao của tam giác ABC là đường trung trực của tam giác DEF
Cho tam giác ABC qua mỗi đỉnh A,B,C kẻ các đường thẳng song song với cạh đối diện chúng cắt nhau tạo thành tam giác DEF
a) CMR: A là trung điểm của EF
b)Các đường cao của tam giác ABC là các đường trung trực của tam giác nào?
Cho Tam giác ABC, qua mỗi đỉnh A,B,C vẽ các đường song song với cạnh đối diện, các đường này cắt nhau tạo thành tam giác DEF.
a, Chứng minh CF,AD,BE đồng quy.
b, Chứng minh 3 đường cao của tam giác ABC là 3 đường trung trực của tam giác DEF.
Cho tam giác ABC . Qua các đỉnh của tam giác kẻ đường thẳng song song với cacnhj đối diện chúng cắt nhau tạo thành tam giác DEF.Chứng minh các đường cao của tam giác ABC là đường trung trực của tam giác DEF
Cho mình xin hình vẽ nha
Cho tam giác ABC nhọn.Qua đỉnh A,B,C KẺ Các đường thẳng song song với các cạnh đối diện.các đường thẳng này cắt nhau tại D,E,F.
A,Cm A là trung điểm của EF
B,Cm các đường cao của tam giác abc là đường trung trực của tam giác DEF
Bài 4. Tam giác ABC cân tại A có góc A = 120°, các đường trung trực của AB và AC cắt nhau tại O, căt cạnh BC lần lượt tại E và F Chứng minh E là trực tâm, trọng tâm tam giác OAB và F là trực tâm, trọng tâm tam giác OAC Bài 5. Tam giác ABC. Qua các đinh A, B, C kẻ các đường thắng song song với cạnh đôi diện, chúng cắt nhau tạo thành tam giác DEF. Chứng minh răng các đường cao của tam giác ABC là các đường trung trực của tam giác DEF MECA và lấy điểm N sao c
qua mỗi đỉnh của tam giác kẻ đường song song với cạnh đối diện với nó a ) chứng minh rằng mỗi đường thẳng cắt hai đường thẳng còn lại b ) chứng minh rằng ba giao điểm là ba đỉnh của một tam giác .
