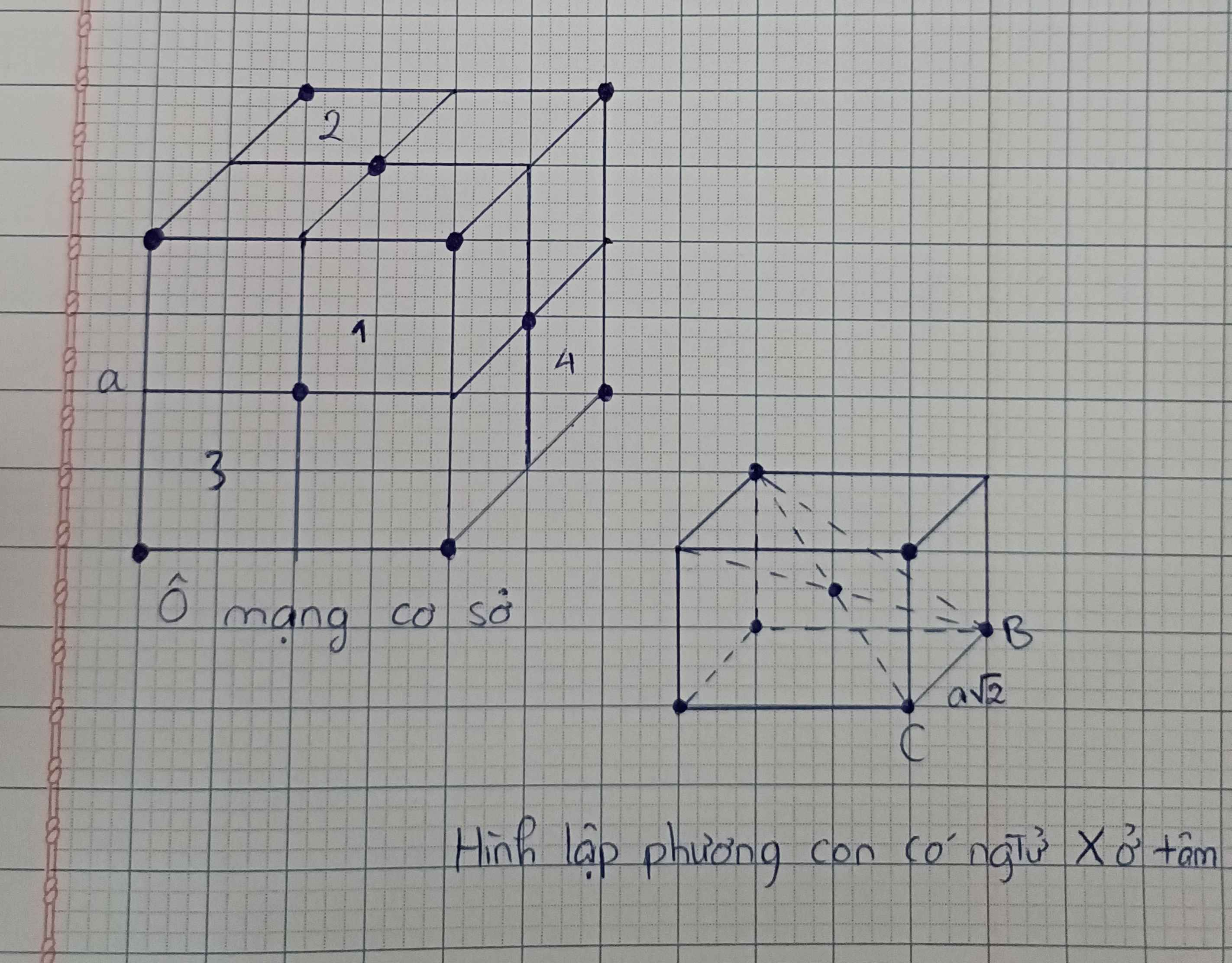
Pin mặt trời chế tạo từ nguyên tố X có khả năng chuyển năng lượng ánh sáng mặt trời thành điện năng, cung cấp cho các thiết bị trên tàu vũ trụ. X có cấu trúc tinh thể lập phương tâm diện với cạnh a của ô mạng cơ sở bằng 5,34 Ao . Nếu mỗi ô mạng cơ sở được chia thành 8 hình lập phương con với cạnh \(\dfrac{\alpha}{2}\) thì có thêm 4 nguyên tử X chiếm 4 tâm của 4 hình lập phương con. Mỗi nguyên tử X trong tinh thể liên kết với 4 nguyên tử X gần nhau nhất bằng các orbital lai hóa sp3 . Khối lượng riêng của X là 2,45 (gam/cm3 ).
a) Tính phần trăm thể tích của tế bào bị chiếm bởi các nguyên tử X.
b) Xác định tên nguyên tố X. Lấy số Avogdro NA = 6,022.1023 nguyên tử/mol
a)
Số nguyên tử trong 1 ô mạng cơ sở là: \(8.\dfrac{1}{8}+6.\dfrac{1}{2}+4=8\left(nguyên.tử\right)\)
Xét 1 hình lập phương con bất kì có tâm là nguyên tử X (chẳng hạn hình lập phương con 1). Theo qui ước nguyên tử ở tâm của hình lập phương con tiếp xúc với 4 nguyên tử ở đỉnh của hình này và chúng được coi là có dạng hình cầu.
Ta có:
\(AC=4r=\sqrt{AB^2+BC^2}=\sqrt{\left(\dfrac{a\sqrt{2}}{2}\right)^2+\left(\dfrac{a}{2}\right)^2}=\dfrac{a\sqrt{3}}{2}\Rightarrow r=\dfrac{a\sqrt{3}}{8}\)
Thể tích của 8 nguyên tử: \(V_{NT}=8.\dfrac{4}{3}.\pi.r^3=\dfrac{32\pi}{3}.\left(\dfrac{a\sqrt{3}}{8}\right)^3=\dfrac{\sqrt{3}.\pi.a^3}{16}\)
Thể tích của 1 ô mạng cơ sở: \(V_{TT}=a^3\)
=> Phần trăm thể tích của tế bào bị chiếm bởi các nguyên tử là:
\(\dfrac{V_{NT}}{V_{TT}}.100\%=\dfrac{\dfrac{\pi a^3\sqrt{3}}{16}}{a^3}.100\%=\dfrac{\sqrt{3}.3,14}{16}.100\%=34\%\)
b)
Khối lượng của 1 ô mạng cơ sở là:
\(m_{NT}=\dfrac{8M_X}{N_A}\left(gam\right)\)
=> Khối lượng riêng của của X: \(d=\dfrac{m_{NT}}{V_{TT}}=\dfrac{8M_X}{a^3.N_A}\)
=> \(M_X=\dfrac{a^3.d.N_A}{8}=\dfrac{\left(5,34.10^{-8}\right)^2.2,45.6,022.10^{23}}{8}=28,083\left(gam/mol\right)\)
=> Vậy X là Silic (Si)