Các câu hỏi tương tự
Trong hệ trục tọa độ Oxy, một elip có độ dài trục lớn là 8, độ dài trục bé là 6 thì có phương trình chính tắc là: A.
x
2
9
+
y
2
16
1
B.
x
2
64
+
y
2...
Đọc tiếp
Trong hệ trục tọa độ Oxy, một elip có độ dài trục lớn là 8, độ dài trục bé là 6 thì có phương trình chính tắc là:
A. x 2 9 + y 2 16 = 1
B. x 2 64 + y 2 36 = 1
C. x 2 16 + y 2 9 = 1
D. x 2 16 + y 2 7 = 1
Trong mặt phẳng tọa độ Oxy, phương trình chính tắc của (E) có độ dài trục lớn bằng 8, trục nhỏ bằng 6 là A.
x
2
64
+
y
2
36
1
B.
x
2
64
+
y
2
9
1
C. ...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, phương trình chính tắc của (E) có độ dài trục lớn bằng 8, trục nhỏ bằng 6 là
A. x 2 64 + y 2 36 = 1
B. x 2 64 + y 2 9 = 1
C. x 2 9 + y 2 9 = 1
D. x 2 16 + y 2 9 = 1
Một vật thể có hai đáy trong đó đáy lớn là một elip có độ dài trục lớn là 8, trục bé là 4 và đáy bé có độ dài trục lớn là 4, trục bé là 2. Thiết diện vuông góc với trục của elip luôn là một elip. Biết chiều cao của vật thể là 4, tính thể tích vật thể A.
55
3
π
B.
56
3
π
C.
57
3
π
D.
58
3
π
Đọc tiếp
Một vật thể có hai đáy trong đó đáy lớn là một elip có độ dài trục lớn là 8, trục bé là 4 và đáy bé có độ dài trục lớn là 4, trục bé là 2. Thiết diện vuông góc với trục của elip luôn là một elip. Biết chiều cao của vật thể là 4, tính thể tích vật thể

A. 55 3 π
B. 56 3 π
C. 57 3 π
D. 58 3 π
Đường cong parabol
y
x
2
6
chia đường elip (E) có độ dài trục lớn và trục bé lần lượt bằng 4 và 2 thành hai phần có tỉ số diện tích bằng (tham khảo hình vẽ bên) A.
S
1
S
2
2
3
5
B.
S...
Đọc tiếp
Đường cong parabol y = x 2 6 chia đường elip (E) có độ dài trục lớn và trục bé lần lượt bằng 4 và 2 thành hai phần có tỉ số diện tích bằng (tham khảo hình vẽ bên)
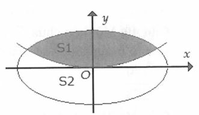
A. S 1 S 2 = 2 3 5
B. S 1 S 2 = 2 π + 3 4 π - 3
C. S 1 S 2 = 4 π + 3 8 π - 3
D. S 1 S 2 = 3 2
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x+2y-z+160 và mặt cầu (s): (x-2)2 + (y+1)2 + (z-3)29. Điểm M di động trên trên (S) và điểm N di động trên (P) sao cho độ dài đoạn thẳng MN ngắn nhất. Tọa độ điểm M là A. M(0;1;-1) B. M(0;-3;4) C. M(2;0;1) D. M(-2;2;-3)
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x+2y-z+16=0 và mặt cầu (s): (x-2)2 + (y+1)2 + (z-3)2=9. Điểm M di động trên trên (S) và điểm N di động trên (P) sao cho độ dài đoạn thẳng MN ngắn nhất. Tọa độ điểm M là
A. M(0;1;-1)
B. M(0;-3;4)
C. M(2;0;1)
D. M(-2;2;-3)
Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng
d
:
x
-
2
2
y
-
1
z
4
và mặt cầu (S): (x-1)2+ (y-2)2 + (z-1)22. Hai mặt phẳng (P), (Q) chứa d và tiếp xúc với (S). Gọi M và N là tiếp điểm. Độ dài đoạn thẳng MN bằng
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng d : x - 2 2 = y - 1 = z 4 và mặt cầu (S): (x-1)2+ (y-2)2 + (z-1)2=2. Hai mặt phẳng (P), (Q) chứa d và tiếp xúc với (S). Gọi M và N là tiếp điểm. Độ dài đoạn thẳng MN bằng
![]()
![]()
![]()
![]()
Cho hàm số y f(x) (ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là A. x – 3y +2 0 B. x + 3y +2 0 C. x – 3y - 2 0 D. x + 3y -2 0
Đọc tiếp
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0
Trong không gian với hệ trục toạ độ (Oxyz), cho mặt cầu
(
S
)
:
(
x
-
1
)
2
+
(
y
-
2
)
2
+
(
z
-
3
)
2
9
điểm A(0;0;2). Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S) theo thiết diện là hình tròn (C) có diện tích nhỏ...
Đọc tiếp
Trong không gian với hệ trục toạ độ (Oxyz), cho mặt cầu ( S ) : ( x - 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 9 điểm A(0;0;2). Phương trình mặt phẳng (P) đi qua A và cắt mặt cầu (S) theo thiết diện là hình tròn (C) có diện tích nhỏ nhất là
A. ( P ) : x + 2 y + 3 z + 6 = 0
B. ( P ) : x + 2 y + z - 2 = 0
C. ( P ) : x - 2 y + z - 6 = 0
D. ( P ) : 3 x + 2 y + 2 z - 4 = 0
Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d có phương trình
x
6
+
t
y
-
2
-
5
t
z...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng d có phương trình x = 6 + t y = - 2 - 5 t z = - 1 + t . Xét đường thẳng ∆ : x - a 5 = y - 1 - 12 = z + 5 - 1 , với a là tham số thực. Tìm tất cả các giá trị của a để đường thẳng d và ∆ cắt nhau.
A. a = 0
B. a = 4
C. a = 8
D. a = 1 2




