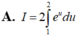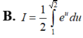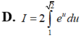a) u 2 + v 2 = u 2 − ( i v ) 2 = (u − iv)(u + iv)
b) u 4 − v 4 = ( u 2 − v 2 )( u 2 + v 2 )
= (u − v)(u + v)(u − iv)(u + iv)
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Phân tích thành nhân tử trên tập số phức: u 4 - v 4
Phân tích thành nhân tử trên tập số phức: u 2 + v 2
Cho số phức u và v. Xét các mệnh đề dưới đây1.
u
+
v
u
+
v
2.
u
−
v
u
−
v
3.
u
.
v
u
.
v
4. ...
Đọc tiếp
Cho số phức u và v. Xét các mệnh đề dưới đây
1. u + v = u + v
2. u − v = u − v
3. u . v = u . v
4. u v = u v v ≠ 0
Hỏi có bao nhiêu mệnh đề đúng trong 4 mệnh đề trên?
A. 1
B. 2
C. 3
D. 4
Phân tích đa thức thành nhân tử
a. -X4 +8X2 -1=0
b. X4 -2X2 +2=0
Trong không gian Oxyz, cho hai vectơ
u
→
(3; 4; 0),
v
→
(2; -1; 2) . Tích vô hướng của hai vectơ
u
→
và
v
→
là: A. 15 B. 2 C. 3 D. 0
Đọc tiếp
Trong không gian Oxyz, cho hai vectơ u → = (3; 4; 0), v → = (2; -1; 2) . Tích vô hướng của hai vectơ u → và v → là:
A. 15
B. 2
C. 3
D. 0
Trong không gian Oxyz, cho hai vectơ
u
→
(-1; 3; 4),
v
→
(2; -1; 5). Tích có hướng của hai vectơ
u
→
và
v
→
là: A.
u
→
,
v
→...
Đọc tiếp
Trong không gian Oxyz, cho hai vectơ u → = (-1; 3; 4), v → = (2; -1; 5). Tích có hướng của hai vectơ u → và v → là:
A. u → , v → = 19 ; 13 ; - 5
B. u → , v → = 19 ; - 13 ; - 5
C. u → , v → = - 19 ; 13 ; - 5
D. u → , v → = 19 ; 13 ; 5
11. Tính tích u×v với u,v là: 11.1 (2,−3,2),e1 + 2e2 −e3.
11.2 ae1 + be2,ce1 + de2.
12. Tính diện tích hình bình hành có ba đỉnh liên tiếp là:
12.1 (1,−2,3),(2,0,1),(0,4,0).
12.2 (1,0,0),(0,b,0),(0,0,1).
Cho điểm M nằm trên cạnh SA, điểm N nằm trên cạnh SB của hình chóp tam giác S. ABC sao cho
S
M
M
A
1
2
,
S
N
N
B
2
. Mặt phẳng (α) qua MN và song song với SC chia khối chóp thành 2 phần. Gọi V₁ là thể tích của khối đa di...
Đọc tiếp
Cho điểm M nằm trên cạnh SA, điểm N nằm trên cạnh SB của hình chóp tam giác S. ABC sao cho S M M A = 1 2 , S N N B = 2 . Mặt phẳng (α) qua MN và song song với SC chia khối chóp thành 2 phần. Gọi V₁ là thể tích của khối đa diện chứa A, V₂ là thể tích của khối đa diện còn lại. Tính tỉ số V 1 V 2
A. V 1 V 2 = 4 5
B. V 1 V 2 = 5 4
C. V 1 V 2 = 5 6
D. V 1 V 2 = 6 5
Xét tích phân
I
∫
1
2
x
e
x
2
d
x
. Sử dụng phương pháp đổi biến số với
u
x
2
, tích phân I được biến đổi thành dạng nào sau đây:
Đọc tiếp
Xét tích phân I = ∫ 1 2 x e x 2 d x . Sử dụng phương pháp đổi biến số với u = x 2 , tích phân I được biến đổi thành dạng nào sau đây:
