Các câu hỏi tương tự
Để định vị một trụ điện, người ta cần đúc một khối bê tông có chiều cao
h
1
,
5
m
gồm:- Phần dưới có dạng hình trụ bán kính đáy
R
1
m
và có chiều cao bằng
1
3
h
;- Phần trên có dạng hình nón bán kính đáy bằng R đã bị cắt bỏ bớt một phần hình nón có bán kính đáy bằng
1
2
R
ở phía trên (ngườ...
Đọc tiếp
Để định vị một trụ điện, người ta cần đúc một khối bê tông có chiều cao h = 1 , 5 m gồm:
- Phần dưới có dạng hình trụ bán kính đáy R = 1 m và có chiều cao bằng 1 3 h ;
- Phần trên có dạng hình nón bán kính đáy bằng R đã bị cắt bỏ bớt một phần hình nón có bán kính đáy bằng 1 2 R ở phía trên (người ta thường gọi hình đó là hình nón cụt);
- Phần ở giữa rỗng có dạng hình trụ bán kính đáy bằng 1 4 R (tham khảo hình vẽ bên dưới).
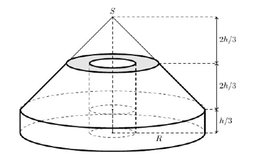
Thể tích của khối bê tông (làm tròn đến chữ số thập phân thứ ba) bằng
A. 2 , 815 m 3
B. 2 , 814 m 3
C. 3 , 403 m 3
D. 3 , 109 m 3
Người ta xây một bể nước hình trụ (tham khảo hình vẽ bên) có bán kính R 1m (tính từ tâm bể đến mép ngoài), chiều dày của thành bể là
b
0
,
05
m
, chiều cao của bể là
h
1
,
5
m
. Tính dung tích của bể nước (làm tròn đến hai chữ số thập phân). A. 4,26
m
3
B. 4,25
m
3...
Đọc tiếp
Người ta xây một bể nước hình trụ (tham khảo hình vẽ bên) có bán kính R = 1m (tính từ tâm bể đến mép ngoài), chiều dày của thành bể là b = 0 , 05 m , chiều cao của bể là h = 1 , 5 m . Tính dung tích của bể nước (làm tròn đến hai chữ số thập phân).
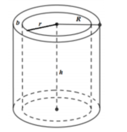
A. 4,26 m 3
B. 4,25 m 3
C. 4,27 m 3
D. 4,24 m 3
Một tấm bìa hình chữ nhật có chiều dài 40cm và chiều rộng 10cm được cắt thành hai phần. Một phần được uốn thành hình hộp chữ nhật có hai đáy là hình vuông cạnh a, phần còn lại được uốn thành hình trụ có hai đáy là hình tròn bán kính r (không tính hai đáy của hình hộp chữ nhật và hình trụ) như hình vẽ sao cho tổng thể tích của hình hộp chữ nhật và hình trụ là nhỏ nhất. Khi đó tổng (a+r) gần giá trị nào nhất trong các giá trị sau? A. 8,3 cm B. 8,4 cm C. 8,5 cm D. 8,6 cm
Đọc tiếp
Một tấm bìa hình chữ nhật có chiều dài 40cm và chiều rộng 10cm được cắt thành hai phần. Một phần được uốn thành hình hộp chữ nhật có hai đáy là hình vuông cạnh a, phần còn lại được uốn thành hình trụ có hai đáy là hình tròn bán kính r (không tính hai đáy của hình hộp chữ nhật và hình trụ) như hình vẽ sao cho tổng thể tích của hình hộp chữ nhật và hình trụ là nhỏ nhất. Khi đó tổng (a+r) gần giá trị nào nhất trong các giá trị sau?
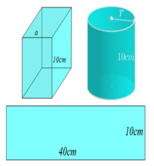
A. 8,3 cm
B. 8,4 cm
C. 8,5 cm
D. 8,6 cm
Một tấm bìa hình chữ nhật có chiều dài 40cm và chiều rộng 10cm được cắt thành hai phần. Một phần được uốn thành hình hộp chữ nhật có hai đáy là hình vuông cạnh a, phần còn lại được uốn thành hình trụ có hai đáy là hình tròn bán kính r (không tính hai đáy của hình hộp chữ nhật và hình trụ) như hình vẽ sao cho tổng thể tích của khối hộp chữ nhật và khối trụ là nhỏ nhất. Khi đó tổng (a+r) gần giá trị nào nhất trong các giá trị sau? A. 8,3cm. B. 8,4cm. C. 8,5cm. D. 8,6cm.
Đọc tiếp
Một tấm bìa hình chữ nhật có chiều dài 40cm và chiều rộng 10cm được cắt thành hai phần. Một phần được uốn thành hình hộp chữ nhật có hai đáy là hình vuông cạnh a, phần còn lại được uốn thành hình trụ có hai đáy là hình tròn bán kính r (không tính hai đáy của hình hộp chữ nhật và hình trụ) như hình vẽ sao cho tổng thể tích của khối hộp chữ nhật và khối trụ là nhỏ nhất. Khi đó tổng (a+r) gần giá trị nào nhất trong các giá trị sau?
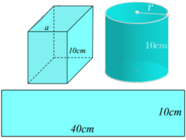
A. 8,3cm.
B. 8,4cm.
C. 8,5cm.
D. 8,6cm.
Cho hình trụ có hai đáy là hai hình tròn
O
và
O
, chiều cao
h
a
3
và bán kính đáy
R
a
. Một hình nón có đỉnh là O và đáy là hình tròn . Tỉ số diện tích xung quanh của hình trụ và hình nón bằng A. 3 B.
2
C. 2 D.
3
Đọc tiếp
Cho hình trụ có hai đáy là hai hình tròn O và O ' , chiều cao h = a 3 và bán kính đáy R = a . Một hình nón có đỉnh là O' và đáy là hình tròn . Tỉ số diện tích xung quanh của hình trụ và hình nón bằng
A. 3
B. 2
C. 2
D. 3
Cho hình trụ có chiều cao h 5, bán kính đáy r 2. Một đoạn thẳng có chiều dài bằng 6 và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách d từ đoạn thẳng đó đến trục của hình trụ. A.
d
11
2
B. d 2 C.
d
5
2
D.
d
4
2
Đọc tiếp
Cho hình trụ có chiều cao h = 5, bán kính đáy r = 2. Một đoạn thẳng có chiều dài bằng 6 và có hai đầu mút nằm trên hai đường tròn đáy. Tính khoảng cách d từ đoạn thẳng đó đến trục của hình trụ.
A. d = 11 2
B. d = 2
C. d = 5 2
D. d = 4 2
Một hộp đựng phần hình hộp chữ nhật có chiều dài 30cm, chiều rộng 5cm và chiều cao 6cm. Người ta xếp thẳng đứng vào đó các viên phấn giống nhau, mỗi viên phấn là khối trụ có chiều cao 6cm và bán kính đáy
r
1
2
c
m
.
Hỏi có thể xếp được tối đa bao nhiêu viên phấn. A. 150 viên B. 153 viên C. 151 viên D. 154 viên
Đọc tiếp
Một hộp đựng phần hình hộp chữ nhật có chiều dài 30cm, chiều rộng 5cm và chiều cao 6cm. Người ta xếp thẳng đứng vào đó các viên phấn giống nhau, mỗi viên phấn là khối trụ có chiều cao 6cm và bán kính đáy r = 1 2 c m . Hỏi có thể xếp được tối đa bao nhiêu viên phấn.
A. 150 viên
B. 153 viên
C. 151 viên
D. 154 viên
Một hình trụ có bán kính đường tròn đáy là r và chiều cao
h
r
3
Lấy hai điểm A, B nằm trên đường tròn đáy của hình trụ sao cho góc giữa đường thẳng AB và hình trụ bằng
30
°
. Khi đó khoảng cách giữa đường thẳng AB với trục của hình trụ bằng A.
r
3
B.
r
3
2
C.
r...
Đọc tiếp
Một hình trụ có bán kính đường tròn đáy là r và chiều cao h = r 3 Lấy hai điểm A, B nằm trên đường tròn đáy của hình trụ sao cho góc giữa đường thẳng AB và hình trụ bằng 30 ° . Khi đó khoảng cách giữa đường thẳng AB với trục của hình trụ bằng
A. r 3
B. r 3 2
C. r 3 3
D. r 6 2
Một hình trụ có chiều cao h và bán kính đáy R. Hình nón có đỉnh là tâm đáy trên của hình trụ và đáy là hình tròn đáy dưới của hình trụ. Gọi
V
1
là thể tích của hình trụ,
V
2
là thể tích của hình nón. Tính tỉ số
V
1
V
2
A. 2 B.
2
2
C. 3 D.
1...
Đọc tiếp
Một hình trụ có chiều cao h và bán kính đáy R. Hình nón có đỉnh là tâm đáy trên của hình trụ và đáy là hình tròn đáy dưới của hình trụ. Gọi V 1 là thể tích của hình trụ, V 2 là thể tích của hình nón. Tính tỉ số V 1 V 2
A. 2
B. 2 2
C. 3
D. 1 3




