Question

nhờ thầy cô giáo và các bạn giải giúp mình , mình cảm ơn

 

Answer 1

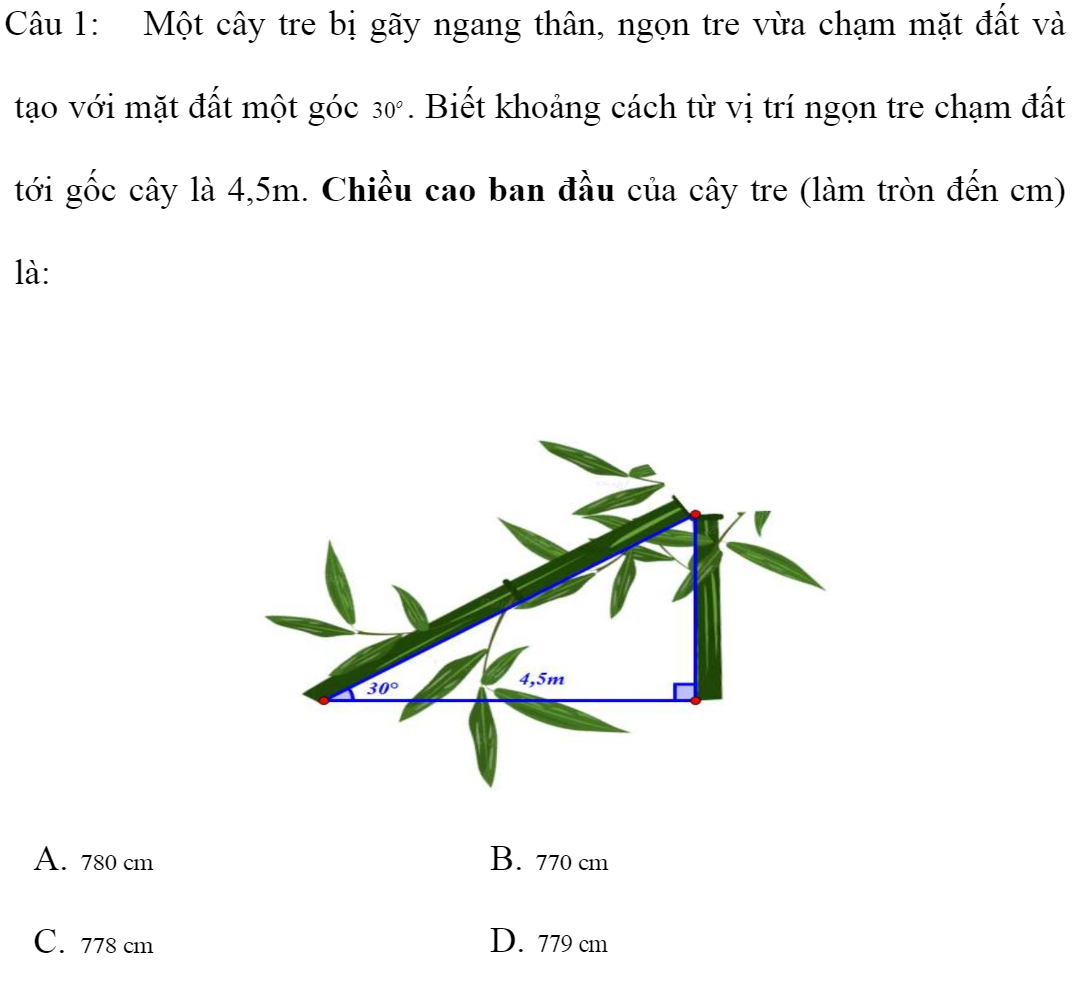
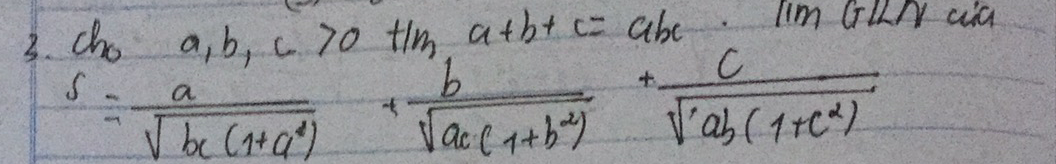Lời giải:
$a+b+c=abc$

$\Rightarrow a(a+b+c)=a^2bc$

$\Rightarrow a(a+b+c)+bc=a^2bc+bc$ hay $(a+b)(a+c)=bc(a^2+1)$

$\Rightarrow \frac{a}{\sqrt{bc(1+a^2)}}=\frac{a}{\sqrt{(a+b)(a+c)}}$
Hoàn toàn tương tự với các phân thức còn lại và cộng theo vế:
\(S=\sum \frac{a}{\sqrt{(a+b)(a+c)}}\leq \sum \frac{1}{2}(\frac{a}{a+b}+\frac{a}{a+c})=\frac{3}{2}\)

Vậy $S_{\max}=\frac{3}{2}$ khi $a=b=c=\sqrt{3}$