Nhờ mọi người giải bài này giúp e với ạ, cảm ơn mọi người nhiều 🫶🏻
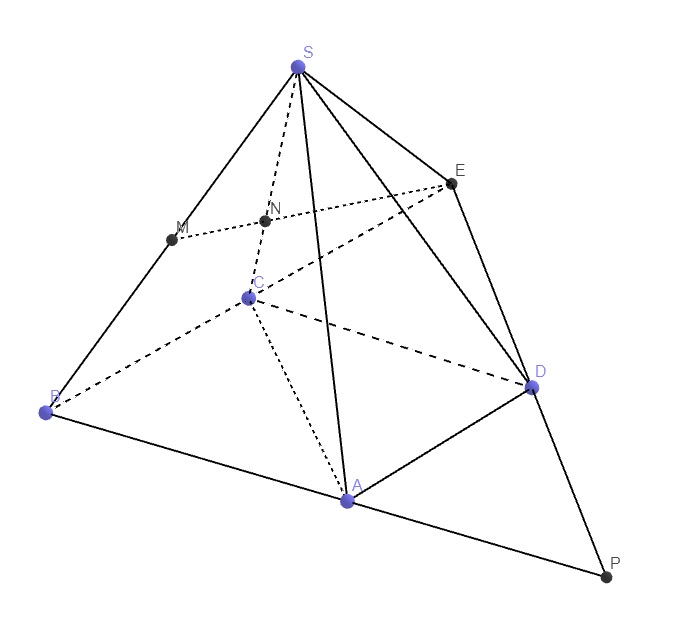
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SB, N là điểm thuộc cạnh SC sao cho SN = 2NC.
a) Chứng minh đường thẳng AC song song với mặt phẳng (DMN)
b) Xác định giao điểm P của đường thẳng AB với mặt phẳng (DMN). Tính tỉ số PA PB
a.
Trng mp (SBC), nối MN kéo dài cắt BC tại E \(\Rightarrow E\in\left(DMN\right)\)
Đặt \(BE=kEC\Rightarrow\overrightarrow{EB}=k.\overrightarrow{EC}\)
M là trung điểm SB \(\Rightarrow\overrightarrow{EM}=\dfrac{1}{2}\overrightarrow{ES}+\dfrac{1}{2}\overrightarrow{EB}=\dfrac{1}{2}\overrightarrow{ES}+\dfrac{k}{2}\overrightarrow{EC}\)
\(\overrightarrow{EN}=\overrightarrow{ES}+\overrightarrow{SN}=\overrightarrow{ES}+\dfrac{2}{3}\overrightarrow{SC}=\overrightarrow{ES}+\dfrac{2}{3}\left(\overrightarrow{SE}+\overrightarrow{EC}\right)\)
\(=\dfrac{1}{3}\overrightarrow{ES}+\dfrac{2}{3}\overrightarrow{EC}\)
E, M, N thẳng hàng \(\Rightarrow\dfrac{\dfrac{1}{2}}{\dfrac{1}{3}}=\dfrac{\dfrac{k}{2}}{\dfrac{2}{3}}\Rightarrow k=2\)
\(\Rightarrow C\) là trung điểm BE \(\Rightarrow CE=BC=AD\)
\(\Rightarrow ADEC\) là hình bình hành (cặp cạnh đối song song và bằng nhau)
\(\Rightarrow AC||DE\)
Mà \(DE\in\left(DMN\right)\Rightarrow AC||\left(DMN\right)\)
b.
Trong mp (ABCD), nối ED kéo dài cắt AB tại P
\(\left\{{}\begin{matrix}P\in AB\\P\in ED\in\left(DMN\right)\end{matrix}\right.\) \(\Rightarrow P=AB\cap\left(DMN\right)\)
Theo cmt, C là trung điểm BE
Mà \(CD||AB\left(gt\right)\Rightarrow CD\) là đường trung bình tam giác EBP
\(\Rightarrow CD=\dfrac{1}{2}BP\)
Lại có ABCD là hình bình hành nên \(CD=AB\)
\(\Rightarrow CD=\dfrac{1}{2}BP=\dfrac{1}{2}\left(AB+AP\right)=\dfrac{1}{2}\left(CD+AP\right)\)
\(\Rightarrow AP=CD=\dfrac{1}{2}BP\)
\(\Rightarrow\dfrac{AP}{BP}=\dfrac{1}{2}\)