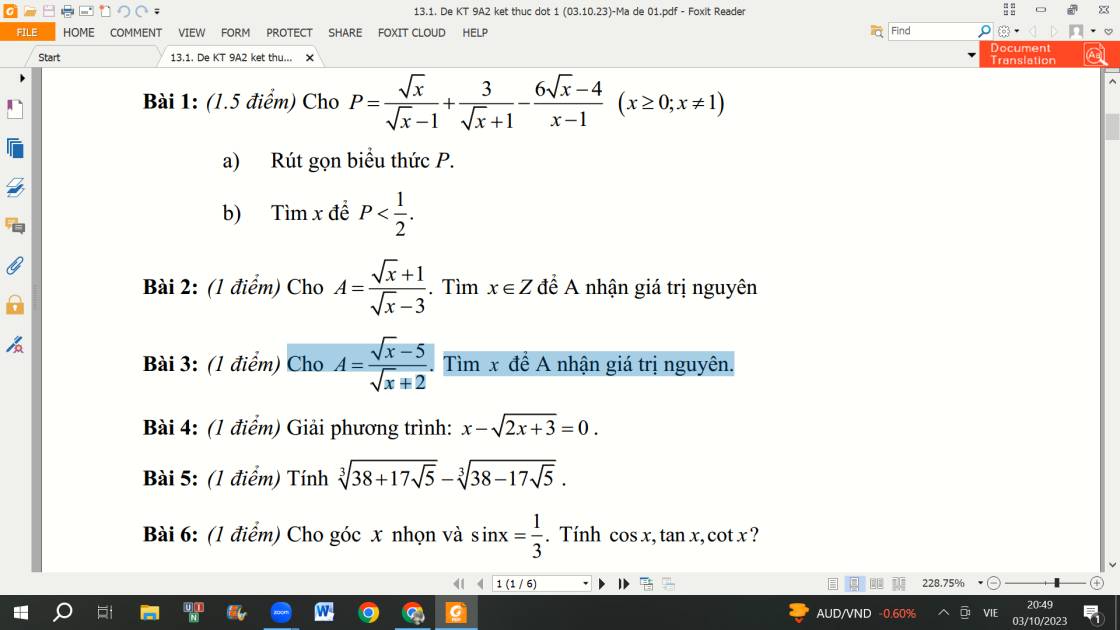
a: \(3x-12-4\sqrt{x}+8=6\sqrt{2x+1}-18\)
=>\(\left(x-4\right)\cdot3-4\left(\sqrt{x}-2\right)=6\left(\sqrt{2x+1}-3\right)\)
=>\(3\left(x-4\right)-\dfrac{4\left(x-4\right)}{\sqrt{x}+2}-6\cdot\dfrac{2x+1-9}{\sqrt{2x+1}+3}=0\)
=>\(\left(x-4\right)\left(3-\dfrac{4}{\sqrt{x}+2}-\dfrac{12}{\sqrt{2x+1}+3}\right)=0\)
=>x-4=0
=>x=4
b: \(\Leftrightarrow\sqrt{x^2+x-1}-1+\sqrt{x-x^2+1}-1=x^2-x\)
=>\(\dfrac{x^2+x-1-1}{\sqrt{x^2+x-1}+1}+\dfrac{x-x^2+1-1}{\sqrt{x-x^2+1}+1}=x\left(x-1\right)\)
=>\(\dfrac{\left(x+2\right)\left(x-1\right)}{\sqrt{x^2+x-1}+1}-\dfrac{x\left(x-1\right)}{\sqrt{x-x^2+1}+1}-x\left(x-1\right)=0\)
=>\(\left(x-1\right)\left(\dfrac{x+2}{\sqrt{x^2+x-1}+1}-\dfrac{x}{\sqrt{x-x^2+1}+1}-x\right)=0\)
=>x-1=0
=>x=1
c: \(\Leftrightarrow x^2-\sqrt{x^3-x^2}-\sqrt{x^2-x}=0\)
=>\(\sqrt{x}\left(x\sqrt{x}-\sqrt{x^2-x}-\sqrt{x-1}\right)=0\)
=>căn x=0
=>x=0

 Nhờ mn giúp em vs ạ. c.ơn nhìu
Nhờ mn giúp em vs ạ. c.ơn nhìu