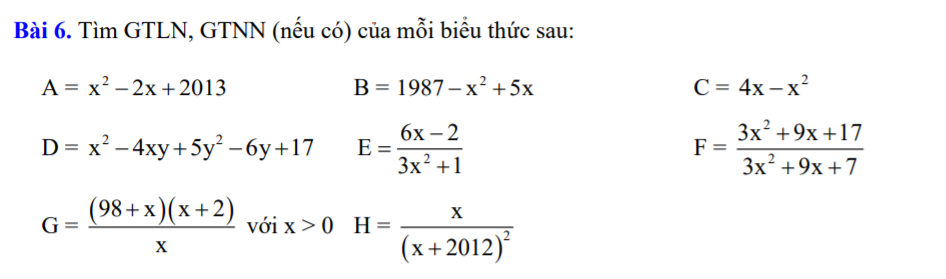\(A=\left(x^2-2x+1\right)+2013=\left(x-1\right)^2+2013\ge2013\\ A_{min}=2013\Leftrightarrow x=1\\ B=-\left(x^2-5x+\dfrac{25}{4}\right)+1993,25=-\left(x-\dfrac{5}{2}\right)^2+1993,25\le1993,25\\ B_{max}=1993,25\Leftrightarrow x=\dfrac{5}{2}\\ C=-\left(x^2-4x+4\right)+4=-\left(x-2\right)^2+4\le4\\ C_{max}=4\Leftrightarrow x=2\\ D=\left(x^2-4xy+4y^2\right)+\left(y^2-6y+9\right)+8\\ D=\left(x-2y\right)^2+\left(y-3\right)^2+8\ge8\\ D_{min}=8\Leftrightarrow\left\{{}\begin{matrix}x=2y=6\\y=3\end{matrix}\right.\)
\(E=\dfrac{6x-2}{3x^2+1}=\dfrac{3x^2+1-3x^2+6x-3}{3x^2+1}=1-\dfrac{3\left(x-1\right)^2}{3x^2+1}\le1\\ E_{max}=1\Leftrightarrow3\left(x-1\right)^2=0\Leftrightarrow x=1\\ F=1+\dfrac{10}{3x^2+9x+7}\\ \text{Có }3x^2+9x+7=3\left(x+\dfrac{3}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\\ \Leftrightarrow F\le1+\dfrac{10}{\dfrac{1}{4}}=41\\ F_{max}=41\Leftrightarrow x=-\dfrac{3}{2}\)
\(G=\dfrac{x^2+100x+196}{x}=x+100+\dfrac{196}{x}\\ \Leftrightarrow G\ge2\sqrt{x\cdot\dfrac{196}{x}}+100=2\cdot14+100=128\\ \Leftrightarrow G_{max}=128\Leftrightarrow x^2=196\Leftrightarrow x=14\left(x>0\right)\\ H=\dfrac{x}{\left(x+2012\right)^2}=\dfrac{x}{x^2+4024x+2012^2}\\ \Leftrightarrow Hx^2+\left(4024\cdot H-1\right)x+2012^2=0\\ \Delta\ge0\Leftrightarrow\left(4024\cdot H-1\right)^2-4\cdot2012^2\cdot H\ge0\\ \Leftrightarrow4024^2H^2-8048\cdot H+1-4024^2\ge0\\ \Leftrightarrow\left[{}\begin{matrix}H\le\dfrac{4025}{4024}\\H\ge-\dfrac{4023}{4024}\end{matrix}\right.\\ \text{Vậy H ko có min hay max}\)