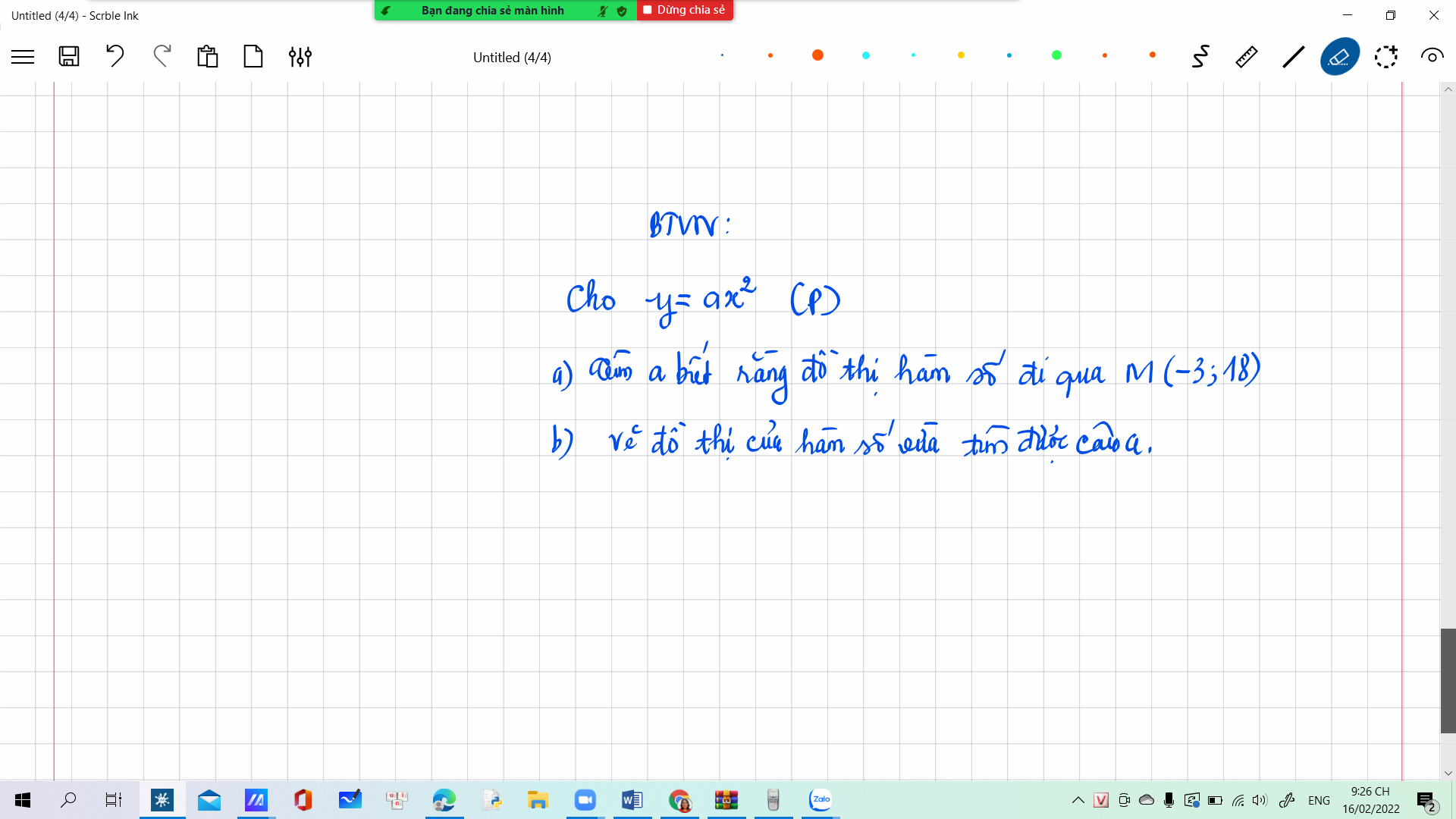
\(a,\left\{{}\begin{matrix}x+y=3\\x^2+y^2+xy=2m+1\end{matrix}\right.\)
Thay m = 3 vào hpt trên ta được hệ mới :
\(\left\{{}\begin{matrix}x+y=3\\x^2+y^2+xy=7\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x+y=3\\\left(x+y\right)^2-xy=7\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x+y=3\\9-xy=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=3-x\\-x\left(3-x\right)+2=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y=3-x\\x^2-3x+2=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y=3-x\\\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\\\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\end{matrix}\right.\)
Vậy \(S=\left\{\left(1;2\right);\left(2;1\right)\right\}\) khi \(m=3\)