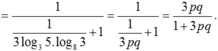Các câu hỏi tương tự
Đặt log 3 p và log 5 q Hãy biểu diễn log1530 theo p và q A. B. C. D.
Đọc tiếp
Đặt log 3= p và log 5= q Hãy biểu diễn log1530 theo p và q
A.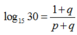 
B.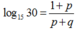 
C.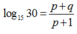 
D.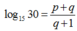 
log3(3+sqrt{3}) log4xLeftrightarrowlog3(3+sqrt{3}) log3x : log34Leftrightarrowlog3(3+sqrt{3}).log34 log3xLeftrightarrowlog3(left(3+sqrt{3}right)^{log_{ }_34} log3xLeftrightarrowx left(3+sqrt{3}right)^{log_34}ko có đt nên tớ làm trong này
Đọc tiếp
log3(\(3+\sqrt{3}\)) > log4x
\(\Leftrightarrow\)log3(\(3+\sqrt{3}\)) > log3x : log34
\(\Leftrightarrow\)log3(\(3+\sqrt{3}\)).log34 > log3x
\(\Leftrightarrow\)log3(\(\left(3+\sqrt{3}\right)^{log_{ }_34}\)> log3x
\(\Leftrightarrow\)x < \(\left(3+\sqrt{3}\right)^{log_34}\)
ko có đt nên tớ làm trong này
Câu 1: Cho đường thẳng (d) xác định bởi hept{begin{cases}y-1x+z0end{cases}}và hai mặt phẳng (P): x+2y+2z+30,(Q): x+2y+2z+70.(Chọn đáp án đúng) Phương trình mặt cầu có tâm thuộc (d) và tiếp xúc với (P), (Q) là:a)left(x+3right)^2+left(y+1right)^2+left(z+3right)^2frac{4}{9}b)left(x+3right)^2+left(y+1right)^2+left(z-3right)^2frac{4}{9}c)left(x-3right)^2+left(y+1right)^2+left(z+3right)^2frac{4}{9}d)left(x-3right)^2+left(y-1right)^2+left(z+3right)^2frac{4}{9}Câu 2: Cho mặt cầu (S): x^2+y^2+z^2-2x+2y+1...
Đọc tiếp
Câu 1: Cho đường thẳng (d) xác định bởi \(\hept{\begin{cases}y=-1\\x+z=0\end{cases}}\)và hai mặt phẳng (P): \(x+2y+2z+3=0,\)(Q): \(x+2y+2z+7=0\).
(Chọn đáp án đúng) Phương trình mặt cầu có tâm thuộc (d) và tiếp xúc với (P), (Q) là:
\(a)\left(x+3\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
\(b)\left(x+3\right)^2+\left(y+1\right)^2+\left(z-3\right)^2=\frac{4}{9}\)
\(c)\left(x-3\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
\(d)\left(x-3\right)^2+\left(y-1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
Câu 2: Cho mặt cầu (S): \(x^2+y^2+z^2-2x+2y+1=0\)và điểm \(M\left(0;-1;0\right).\)
Phương trình mặt phẳng (P) tiếp xúc với (S) tại M là:
\(a)2x+y-z+1=0.\) \(b)x=0.\)
\(c)-x+y+2z+1=0.\) \(d)x+y+1=0\)
Câu 3: Trong khai triển \(f\left(x\right)=\frac{1}{256}\left(2x+3\right)^{10}\)thành đa thức, hệ số của x8 là:
\(a)103680.\) \(b)405.\) \(c)106380.\) \(d)504.\)
Câu 4: Tổng các nghiệm của phương trình \(2^{x^2-3}.5^{x^2-3}=0,01.\left(10^{x-1}\right)^3\)là:
\(a)3.\) \(b)5.\) \(c)0.\) \(d)2\sqrt{2}.\)
Giá trị lớn nhất của: \(y=x^3+5x+7\) trên đoạn \([-5:0]\)bằng:
A. 80
B. -143
C. 5
D. 7
Đặt
log
8
3
p
v
à
log
n
x
3
log
m
x
.
Hãy biểu thị log5 theo p và q A. pq B.
3
p
+
q
5
C.
3
p
+
q...
Đọc tiếp
Đặt log 8 3 = p v à log n x = 3 log m x . Hãy biểu thị log5 theo p và q
A. pq
B. 3 p + q 5
C. 3 p + q 1 + 3 p q
D. 1 + 3 p q p + q
1.Tính các giá trị biểu thức sau:a)510000.log52-59999.log52-...-53.log52-52.log52?b)(x2+1).4100000-(x2+1).499999,5-...-(x2+1).43.5-(x2+1).43?2.Giải ptrình bậc cao sau:a)x.(x2+y)150000-x.(x2+y)149999-...-x.(x2+y)2-x3-xy-20b)xy(2y+1)50000-xy(2y+1)49999-...-xy(2y+1)2-2xy2-30c)x2(x+1)10000-x2(x+1)9999-...-x2(x+1)2-x2(x+1)-x2-10d)x.(sqrt{x+1})10000-x.(sqrt{x+1})9998-...-x.(sqrt{x+1})4-x-303.Tính giá trị tại vị trí gián đoạn sau:a)250000-249999-...-24-23?Biết gián đoạn tại vị trí thứ 4b)710000.log72-7...
Đọc tiếp
1.Tính các giá trị biểu thức sau:
a)510000.log52-59999.log52-...-53.log52-52.log52=?
b)(x2+1).4100000-(x2+1).499999,5-...-(x2+1).43.5-(x2+1).43=?
2.Giải ptrình bậc cao sau:
a)x.(x2+y)150000-x.(x2+y)149999-...-x.(x2+y)2-x3-xy-2=0
b)xy(2y+1)50000-xy(2y+1)49999-...-xy(2y+1)2-2xy2-3=0
c)x2(x+1)10000-x2(x+1)9999-...-x2(x+1)2-x2(x+1)-x2-1=0
d)x.(\(\sqrt{x+1}\))10000-x.(\(\sqrt{x+1}\))9998-...-x.(\(\sqrt{x+1}\))4-x-3=0
3.Tính giá trị tại vị trí gián đoạn sau:
a)250000-249999-...-24-23=?Biết gián đoạn tại vị trí thứ 4
b)710000.log72-79999.log72-...-72.log72-7log72=?Biết gián đoạn tại vị trí 3->5
c)22+23+...+24999+25000=?Biết gián đoạn tại vị trí thứ 350 và vị trí 600
4.Thực hiện các yêu cầu sau:
Cho pt M: x.(x+1)50000-x.(x+1)49999-...-x.(x+1)3-x.(x+1)2-n=0
a.Xác định x=?
b.Tính n=?
c.Số nào dưới đây là số nguyên tố:
A.n+1/n-1
B.n+2/n-2
C.n+3/n-3
D.n+4/n-4
d.Xác định phương trình đồng dạng bậc 20(¶20)?
5.Cho ptrình bậc 2 sau:x2-2x=0
a.Xác định hàm P=?
A.P=(x2)x^2-2x B.P=(x2-2x)/(x2-2x) C.P=2xx^2 D.(x2-2x)x^2-2x
b.Xác định hàm P(x)?Biết Q(x)=2x+1
A.P(x)=2x B.P(x)=2.(x+1) C.P(x)=2.(x+2) D.P(x)=2.(x+3)
c.Tính lim(P/Q(x))=?
A.0 B.1 C.2 D.3
d.Ptrình bậc cao:250000-249999-...-22-21 ~ vs hàm nào cuả pt bậc 2?
A.2P=2.2xx^2-2x B.2P=2.x2.2x C.2P=2.22x D.2P=2.42x
e.Đồ thị hàm bậc cao nằm trên:
A.Trục tung B.Trục hoành C.A,B đúng D.A,C sai
f.Khi nào P=P(x)?
A.Q(x)=0 B.P(x)=0 C.P=0 D.Q(x)=P
g.Hãy biến ptrình bậc 3 sau về ptrình bậc cao:x3-x=0?
A.(x3-x)50000-(x3-x)49999-...-(x3-x)2-x3-x=0
B.(x3-x)50000-(x3-x)49999-...-(x3-x)2-x3+x=0
C.(x3+x)50000-(x3+x)49999-...-(x3+x)2-x3-x=0
D.(x3+x)50000-(x3+x)49999-...-(x3+x)2-x3+x=0
h.Từ ptrình bậc 3 ở câu g so sánh P1=xx^3-x và P2=x3.(x^3-x)
A.P1>P2 B.P1=P2 C.P1<P2 D.P1~P2
i.Từ câu h,hãy tính giá trị biểu thức sin(P1-1)+cos(P2-1)+tan(P1P2-P1-P2+1)=?
A.-3 B.-1 C.1 D.3
Giúp mik với
5 tháng 6 2021 lúc 0:43
Giá trị cực đại của hàm số \(y=x+sin2x\) trên \(\left(0;\pi\right)\)là
\(A.\frac{\pi}{6}+\frac{\sqrt{3}}{2}\)
\(B.\frac{2\pi}{3}+\frac{\sqrt{3}}{2}\)
\(C.\frac{2\pi}{3}-\frac{\sqrt{3}}{2}\)
\(D.\frac{\pi}{3}+\frac{\sqrt{3}}{2}\)
3 tháng 6 2021 lúc 16:08
Cho hàm số \(f\left(x\right)=\frac{1}{5}m^2x^5-\frac{1}{3}mx^3+10x^2-\left(m^2-m-20\right)x\)Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số đồng biến trên R. Tổng giá trị của tất cả các phần tử thuộc S bằng :
A. 3/2
B. -2
C. 5/2
D. 1/2
Cho ba mặt phẳng:
(P): 2x + y + z + 3 = 0
(Q): x - y - z - 1 = 0
(R): y - z + 2 = 0
Khẳng định nào sau đây là sai?
A. Không có điểm nào cùng thuộc ba mặt phẳng trên
B. (P) ⊥ (Q)
C. (P) ⊥ (R)
D. (Q) ⊥ (R)