Đáp án D.
log 7 x = log 7 a b 2 – log 7 a 3 b = log 7 a b 2 a 3 b = log 7 b a - 2
Do đó x = a–2b.
Đáp án D.
log 7 x = log 7 a b 2 – log 7 a 3 b = log 7 a b 2 a 3 b = log 7 b a - 2
Do đó x = a–2b.
Nếu log 7 ( log 3 ( log 2 x ) ) = 0 ( x > 0 ) thì 1 x bằng
![]()
![]()
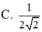
![]()
Nếu log 7 ( log 3 ( log 2 x ) ) = 0 thì x - 1 2 bằng :
A. 1 3
B. 1 42
C. 1 2 2
D. 1 3 3
Biết rằng log 7 = a , log 5 100 = b . Hãy biểu diễn log 25 56 theo a và b.
![]()
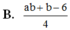
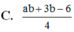
![]()
Nghiệm của phương trình log5x = log7(x + 2) là:
A. 3.
B. 4.
C. 5.
D. 6.
Giải bất phương trình log 7 . x . log 4 5 > 0 . Gọi tập nghiệm là S. Khi đó:
A. Rỗng
B. 0 ; 1
C. 1 , + ∞
D. 1 ; + ∞ / 1
Biết log7 2 = m, khi đó giá trị của log49 28 được tính theo m là:
A. 1 + 2 m 2
B. m + 2 4
C. 1 + m 2
D. 1 + 4 m 2
Cho a, b, c, d là các số nguyên dương thỏa mãn log a b = 3 2 , log c d = 5 4 . Nếu a-c=9, thì b-d nhận giá trị nào?
A. 85.
B. 71.
C. 76.
D. 93.
Đặt log 2 3 = a , log 3 4 = b . Biểu diễn T = log 27 8 + log 256 81 theo a và b ta được T = x a 2 + y b 2 + 4 z a 2 b + a b 2 với x, y, z là các số thực. Hãy tính tổng 4 x 2 + y - z 3
A. 3
B. 4
C. 6
D. 2
Đặt log 2 3 = a , log 3 4 = b . Biểu diễn T = log 27 8 + log 256 81 theo a và b ta được T = x a 2 + y b 2 + 4 z a 2 b + a b 2 với x, y, z là các số thực. Hãy tính tổng 4 x 2 + y - z 3 .
A. 3
B. 4
C. 6
D. 2