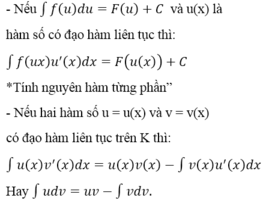
Nguyên hàm
Cho hàm số f(x) xác định trên K ( k là nửa khoảng hay đoạn của trục số). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F’(x) = f(x) với mọi x thuộc K.
Phương pháp tính nguyên hàm
* Đổi biến số:
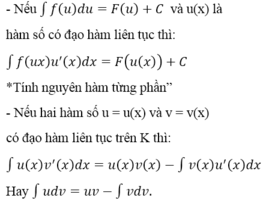
Nêu định nghĩa và các phương pháp tính tích phân.
Nêu phương pháp tính nguyên hàm từng phần. Cho ví dụ minh họa.
Tính các nguyên hàm sau bằng phương pháp đổi biến số:
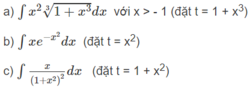
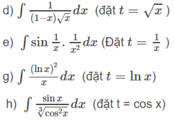
Tính các nguyên hàm sau bằng phương pháp đổi biến số: ∫ ln x 2 x d x (đặt t = lnx)
Tính các nguyên hàm sau bằng phương pháp đổi biến số: ∫ sin x c o s 2 x 3 d x (đặt t = cosx)
Tính các nguyên hàm sau bằng phương pháp đổi biến số: ∫ sin 1 x . 1 x 2 d x (đặt t = 1 x )
Tính các nguyên hàm sau bằng phương pháp đổi biến số: ∫ 1 1 - x x d x (đặt t = x )
Tính các nguyên hàm sau bằng phương pháp đổi biến số: ∫ x . e - x 2 d x (đặt t = x 2 )
Tính các nguyên hàm sau bằng phương pháp đổi biến số: ∫ x 1 + x 2 2 d x (đặt t = 1 + x 2 )
