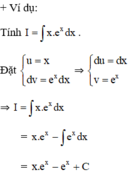
+ Phương pháp nguyên hàm từng phần:
Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên K thì:
∫u(x).v’(x)dx = u(x).v(x) - ∫v(x).u’(x)dx
Hay viết gọn: ∫udv = uv - ∫vdv.
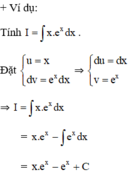
Cho P(x) là đa thức của x. Từ Ví dụ 9, hãy lập bảng theo mẫu dưới đây rồi điền u và dv thích hợp vào chỗ trống theo phương pháp nguyên phân hàm từng phần.
| ∫ P(x) e x dx | ∫ P(x)cosxdx | ∫ P(x)lnxdx |
| P(x) | ||
| e x dx |
Nêu các tính chất của tích phân. Cho ví dụ minh họa.
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính:
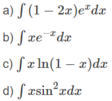
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x sin 2 x d x
Hãy tính ∫ x + 1 e x d x bằng phương pháp tính nguyên hàm từng phần.
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ 1 - 2 x e x d x
Sử dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x . ln 1 + x d x
Áp dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ x e - x d x
Sử dụng phương pháp tính nguyên hàm từng phần, hãy tính: ∫ 1 - x . cos x d x
