Phương pháp:
Tính tích phân bằng phương pháp đổi biến.
Cách giải:
![]()
![]()
![]()
![]()
![]()
Chọn: C
Phương pháp:
Tính tích phân bằng phương pháp đổi biến.
Cách giải:
![]()
![]()
![]()
![]()
![]()
Chọn: C
Với cách biến đổi u = 1 + 3 ln x thì tích phân ∫ 1 e ln x x 1 + 3 ln x trở thành
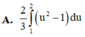
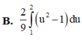
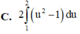
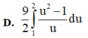
Tính các tích phân sau: 1) 2 ln e e x dx ; 2) 1 3 2 0 4 x dx x ; 3) /2 /4 1 tan dx x ; 4) 1 0 x e dx ; 5) 2 1 x xe dx ; 6) 0 1 3 4 dx x ; 7) 2 1 4 4 5 dx x x ; 8) 2 0 ln 1 x dx x (HD: 1 u x ) ĐS: 1) 2 e ; 2) 16 7 5 3 ; 3) ln 2 ; 4) 2
Tính tích phân I=\(\int\limits^{\pi}_0\)\(x^2cos2xdx\) bằng cách đặt \(\left\{{}\begin{matrix}u=x^2\\dv=cos2xdx\end{matrix}\right.\).Mệnh đề nào dưới đây đúng?
A. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}-\int\limits^{\pi}_0xsin2xdx\)
B. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}-2\int\limits^{\pi}_0xsin2xdx\)
C. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}+\int\limits^{\pi}_0xsin2xdx\)
D. \(I=\dfrac{1}{2}x^2sin2x|^{^{\pi}_0}+2\int\limits^{\pi}_0xsin2xdx\)
Cho tích phân I = ∫ 0 π 2 sin 2 x cos x d x , với t = sin x thì tích phân I trở thành?
A. I = ∫ 0 1 t 2 d t
B. I = 2 ∫ 0 1 t d t
C. I = - ∫ - 1 0 t 2 d t
D. I = - ∫ 0 1 t 2 d t
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Khi đặt t = log5 x thì bất phương trình log 5 2 5 x - 3 log 5 x - 5 ≤ 0 trở thành bất phương trình nào dưới đây?
![]()
![]()
![]()
![]()
Cho hàm số f(x) thỏa mãn ∫ 0 1 ( x + 1 ) f ' ( x ) d x = 10 và 2f(1) - f(0) = 2 .Tính tích phân I = ∫ 0 1 f ( x ) d x .
A. I=-12.
B. I=8.
C. I=12.
D. I=-8
Cho hàm số y = f ( x ) = x 2 k h i 0 ≤ x ≤ 1 2 - x k h i 1 ≤ x ≤ 2
Tính tích phân I= ∫ 0 2 f ( x ) d x
![]()
![]()
![]()
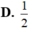
Cho hàm số y = f(x) có đạo hàm f’(x) liên tục trên đoạn [0; 1] thỏa mãn f(1) = 1 và I = ∫ 0 1 f x d x = 2 . Tính tích phân I = ∫ 0 1 f ' x d x
A. I = -1.
B. I = 1.
C. I = 2.
D. I = -2.