\(\frac{a}{b} = \frac{c}{d} \Leftrightarrow a \cdot d = b \cdot c\)
Tính chất dãy tỉ số bằng nhau:\(\frac{a}{b} = \frac{c}{d} = \frac{e}{f} \Rightarrow \frac{a + c + e}{b + d + f} = \frac{a}{b} = \frac{c}{d} = \frac{e}{f}\)
Công thức tính lũy thừa:\(a^{m} \cdot a^{n} = a^{m + n} , \frac{a^{m}}{a^{n}} = a^{m - n} , \left(\right. a^{m} \left.\right)^{n} = a^{m \cdot n}\)
Tính chất căn bậc hai:\(\sqrt{a \cdot b} = \sqrt{a} \cdot \sqrt{b} , \sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}} \left(\right. a , b \geq 0 \left.\right)\)
🔹 2. Hình học phẳngTổng 3 góc trong tam giác:\(\hat{A} + \hat{B} + \hat{C} = 180^{\circ}\)
Tứ giác: Tổng 4 góc = \(360^{\circ}\).Tam giác cân: Hai góc ở đáy bằng nhau.Tam giác đều: 3 cạnh bằng nhau, 3 góc bằng \(60^{\circ}\).Đường trung bình trong tam giác:\(\text{Trung}\&\text{nbsp};\text{b} \overset{ˋ}{\imath} \text{nh}\&\text{nbsp}; = \frac{1}{2} \cdot \text{c}ạ\text{nh}\&\text{nbsp};đ \overset{ˊ}{\text{a}} \text{y}\)
Diện tích tam giác:\(S = \frac{1}{2} \cdot a \cdot h\)
Diện tích hình chữ nhật:\(S = a \cdot b\)
Diện tích hình vuông:\(S = a^{2}\)
Diện tích hình thang:\(S = \frac{\left(\right. a + b \left.\right) \cdot h}{2}\)
Diện tích hình bình hành:\(S = a \cdot h\)
Diện tích hình tròn:\(S = \pi R^{2}\)
Chu vi hình tròn:\(C = 2 \pi R\)
🔹 3. Biểu thức đại sốHằng đẳng thức đáng nhớ:\(\left(\right. a + b \left.\right)^{2} = a^{2} + 2 a b + b^{2}\) \(\left(\right. a - b \left.\right)^{2} = a^{2} - 2 a b + b^{2}\) \(a^{2} - b^{2} = \left(\right. a - b \left.\right) \left(\right. a + b \left.\right)\)
👉 Đây là những công thức cơ bản lớp 7 thường dùng nhất.
\(a + b = c \Leftrightarrow a = c - b\)2. Lũy thừa với số mũ nguyên\(a^{m} \cdot a^{n} = a^{m + n}\)\(\frac{a^{m}}{a^{n}} = a^{m - n}\) (với \(a \neq 0\))\(\left(\right. a^{m} \left.\right)^{n} = a^{m \cdot n}\)\(\left(\right. a b \left.\right)^{n} = a^{n} \cdot b^{n}\)\(\left(\left(\right. \frac{a}{b} \left.\right)\right)^{n} = \frac{a^{n}}{b^{n}}\) (với \(b \neq 0\))3. Biểu thức đại sốQuy tắc khai triển hằng đẳng thức:\(\left(\right. a + b \left.\right)^{2} = a^{2} + 2 a b + b^{2}\)\(\left(\right. a - b \left.\right)^{2} = a^{2} - 2 a b + b^{2}\)\(a^{2} - b^{2} = \left(\right. a - b \left.\right) \left(\right. a + b \left.\right)\)4. Tỉ lệ thức và đại lượng tỉ lệTỉ lệ thức: \(\frac{a}{b} = \frac{c}{d} \Rightarrow a d = b c\)Tính chất dãy tỉ số bằng nhau:
\(\frac{a}{b} = \frac{c}{d} = \frac{e}{f} \Rightarrow \frac{a + c + e}{b + d + f} = \frac{a}{b}\)5. Đại lượng tỉ lệ thuận – tỉ lệ nghịchTỉ lệ thuận: \(y = k x\) (với \(k \neq 0\))Tỉ lệ nghịch: \(y = \frac{k}{x}\) (với \(x \neq 0\), \(k \neq 0\))6. Hàm số và đồ thịHàm số bậc nhất: \(y = a x\)Hàm số đồng biến nếu \(a > 0\)Hàm số nghịch biến nếu \(a < 0\)📐 HÌNH HỌC 71. Hai đường thẳng song songNếu hai đường thẳng cắt một đường thẳng thứ ba và:Hai góc so le trong bằng nhau ⇒ Hai đường thẳng song song.Hai góc đồng vị bằng nhau ⇒ Hai đường thẳng song song.2. Tam giácTổng ba góc trong một tam giác: \(A + B + C = 180^{\circ}\)Các trường hợp bằng nhau của tam giác:Cạnh – Cạnh – Cạnh (CCC)Cạnh – Góc – Cạnh (CGC)Góc – Cạnh – Góc (GCG)3. Các đường trong tam giácĐường trung tuyến: Nối từ một đỉnh đến trung điểm cạnh đối.Đường phân giác: Chia góc ở đỉnh thành hai phần bằng nhau.Đường cao: Vuông góc từ đỉnh đến cạnh đối.Trung trực: Đường thẳng vuông góc với cạnh tại trung điểm.4. Quan hệ giữa các yếu tố trong tam giácBất đẳng thức tam giác:
\(A B + B C > A C , A B + A C > B C , A C + B C > A B\)Trong một tam giác:Góc đối diện cạnh lớn hơn là góc lớn hơn.Cạnh đối diện góc lớn hơn là cạnh dài hơn.
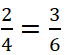
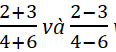với các tỉ số trong tỉ lệ thức đã cho.
