Các câu hỏi tương tự
cho tam giác abc cân tại a, đường cao ah, g là trọng tâm của tam giác abc. Chứng minh a, g, h thẳng hàng
Bài 4: Cho tam giác ABC cân tại A;đường cao AH và đường trung tuyến BK cắt nhau tại G. Tia CG cắt cạnh AB tại điểm I
a) Chứng minh: G là trọng tâm của tam giác ABC. Chứng minh IA=IB
cho tam giác ABC cân tại A. Gọi G là trọng tâm tam giác, I là giao điểm các phân giác của tam giác. Chứng minh: 3 điểm A,G,I thẳng hàng
Cho tam giác ABC cân tại A ,đường cao AK ( K BC)a) Chứng minh: tam giác ABK tam giácACK.b) Gọi M là trung điểm của AB , AK cắt CM tại G. Chứng minh: Chưng minh G là trọng tâm của tam giác ABC .c) Trên tia đối của tia MB lấy điểm N sao cho MN MG.Chứng minh: BN // AK .
Đọc tiếp
Cho tam giác ABC cân tại A ,đường cao AK ( K ![]() BC)
BC)
a) Chứng minh: tam giác ABK = tam giácACK.
b) Gọi M là trung điểm của AB , AK cắt CM tại G. Chứng minh: Chưng minh G là trọng tâm của tam giác ABC .
c) Trên tia đối của tia MB lấy điểm N sao cho MN = MG.Chứng minh: BN // AK
.
Cho tam giác ABC cân tại A ( góc A bé hơn 90 độ ) . Kẻ đường trung tuyến AI a, Chứng minh △ ABI = △ ACI
b, Chứng minh Ai là đường cao của tam giác ABC c, Gọi G là trọng tâm của ABC . Biết Ai = 12cm . Tính Gi d, Gọi D là trung điểm của AC . Chứng minh BC bé hơn 3/4 BD
cho tam giác ABC cân tại A . gọi G là trọng tâm của tam giác . I là giao điểm các phân giác của tam giác . chứng minh: ba điểm A, G,I thẳng hàng
Cho tam giác ABC cân tại A. Gọi G là trọng tâm của tam giác, gọi I là giao điểm các đường phân giác của tam giác. Chứng minh rằng ba điểm A, G, I thẳng hàng.
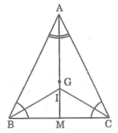
Cho tam giác ABC cân tại A. Gọi G là trọng tâm, O là giao điểm ba đường trung trực của tam giác ABC. a) Tam giác BOC là tam giác gì? b) Chứng minh ba điểm A, O, G thẳng hàng?
cho tam giác ABC cân tại A có A là góc nhọn. vẽ tia phân giác của BAC cắt BC tại H.
a) chứng minh tam giác ABH=ACH
b) vẽ trung tuyến BD của tam giác ABC cắt H tại G. Chứng minh G là trọng tâm tam giác ABC
c) qua H vẽ đường thẳng song song với AC cắt AB tại E. Chứng minh ba điểm C,G,E thẳng hàng
vẽ cả hình











