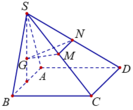
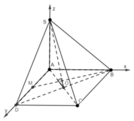
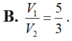Một phần thiết kế của một công trình đang xây dựng có dạng như hình bên, trong đó ABCD là hình vuông cạnh 6 m, AM, BN, DP cùng vuông góc với (ABCD), AM = 4 m, BN= 3 m, DP=2 m. Góc giữa hai mặt phẳng (ABCD) và (MNP) (làm tròn kết quả đến hàng đơn vị của độ) là nº với n là số nguyên dương. Giá trị của n là bao nhiêu?
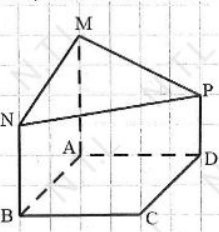
\(MP^2=AD^2+\left(MA-DP\right)^2\Rightarrow MP=\sqrt{6^2+\left(4-2\right)^2}=2\sqrt{10}\)
\(MN=\sqrt{AB^2+\left(MA-BN\right)^2}=\sqrt{6^2+1^2}=\sqrt{37}\)
\(NP=\sqrt{BD^2+\left(BN-DP\right)^2}=\sqrt{2AB^2+1}=\sqrt{73}\)
\(\Rightarrow S_{MNP}=3\sqrt{41}\) (áp dụng công thức Herong)
\(S_{ABD}=\dfrac{1}{2}AB^2=18\)
\(\Rightarrow cos\left(n^0\right)=\dfrac{S_{ABD}}{S_{MNP}}=\dfrac{6\sqrt{41}}{41}\)
\(\Rightarrow n=20\)