Đáp án A.
Ta có f x = F ' x = 2 a x + b - d x 2 e 1 x - a + b x + c x 2 + d x 3 e 1 x = 2 a x + b - a - b x - c x 2 - d x 2 - d x 3 e 1 x ⇒ 2 a = 2 b - a = - 1 b = 0 - c - d = 0 - d = 0 ⇔ a = 1 b = 0 c = 0 d = 0 ⇒ a + b + c + d = 1 .
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho hàm số
f
(
x
)
a
x
+
b
c
x
+
d
với a,b,c,d là các số thực và c
≠
0. Biết f(1)1, f(2)2 và f(f(x))x với mọi
x
≠
-
d
c
. Tính
l
i
m...
Đọc tiếp
Cho hàm số f ( x ) = a x + b c x + d với a,b,c,d là các số thực và c ≠ 0. Biết f(1)=1, f(2)=2 và f(f(x))=x với mọi x ≠ - d c . Tính l i m x → ∞ f ( x ) .
A. 3 2
B. 5 6
C. 2 3
D. 6 5
Xác định giá trị a, b, c để hàm số
F
(
x
)
(
a
x
2
+
b
x
+
c
)
e
-
x
là một nguyên hàm của
f
(
x
)
(
x
2
-
3
x
+
2
)
e...
Đọc tiếp
Xác định giá trị a, b, c để hàm số F ( x ) = ( a x 2 + b x + c ) e - x là một nguyên hàm của f ( x ) = ( x 2 - 3 x + 2 ) e - x
A. a = -1; b = 1; c = -1
B. a = -1; b = -5; c = -7
C. a = 1; b = -3; c = 2
D. a = 1; b = -1; c = 1
Biết hàm số
F
(
x
)
a
x
3
+
(
a
+
b
)
x
2
+
(
2
a
-
b
+
c
)
x
+
1
là một nguyên hàm của hàm số
f
(
x
)
3
x
2
+
6...
Đọc tiếp
Biết hàm số F ( x ) = a x 3 + ( a + b ) x 2 + ( 2 a - b + c ) x + 1 là một nguyên hàm của hàm số f ( x ) = 3 x 2 + 6 x + 2 . Tổng a+b+c là:
A. 5
B. 4
C. 3
D. 2
Cho hàm số
y
f
x
a
x
3
+
b
x
3
+
c
x
+
d
a
,
b
,
c
,
d
∈
ℝ
;
a
≠...
Đọc tiếp
Cho hàm số y = f x = a x 3 + b x 3 + c x + d a , b , c , d ∈ ℝ ; a ≠ 0 biết f'(-1)=3. Tính lim ∆ x → ∞ f 1 + ∆ x + f 1 ∆ x
A. 3
B. -3
C. 1
D. -1
Cho hàm số
f
(
x
)
a
x
4
+
b
x
3
+
c
x
2
+
d
x
+
e
,
(
a
,
b
,
c
,
d
,
e
∈
ℝ
)
Hàm yf(x) có bảng xét dấu như sau: Số nghiệm của phương trình f(x)e là A....
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e , ( a , b , c , d , e ∈ ℝ ) Hàm y=f'(x) có bảng xét dấu như sau:
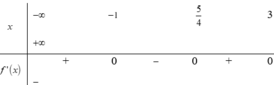
Số nghiệm của phương trình f(x)=e là
A. 1
B. 0
C. 2
D. 3
Biết
F
(
x
)
(
a
x
2
+
b
x
+
c
)
e
-
x
là một nguyên hàm của hàm số
f
(
x
)
(
2
x
2
-
5
x
+
2
)
e
-...
Đọc tiếp
Biết F ( x ) = ( a x 2 + b x + c ) e - x là một nguyên hàm của hàm số f ( x ) = ( 2 x 2 - 5 x + 2 ) e - x trên R. Giá trị của biểu thức f(F(0)) bằng
A. 9e
B. 3e
C. 20 e 2
D. - 1 e
nếu 0<a<b<c<d<e<f
(a-b)(c-d)(e-f).x=(b-a)(d-c)(f-e) thì x=...
Cho hàm số f(x) biết f(0) 1 và
f
x
4
x
2
+
4
x
+
3
2
x
+
1
. Biết nguyên hàm của f(x) có dạng
F
x...
Đọc tiếp
Cho hàm số f(x) biết f(0) = 1 và f x = 4 x 2 + 4 x + 3 2 x + 1 . Biết nguyên hàm của f(x) có dạng
F x = a x 2 + b x + ln 2 x + 1 + c . Tính tỉ lệ a : b : c
A. a : b : c = 1 : 2 : 1
B. a : b : c = 1 : 1 : 1
C. a : b : c = 2 : 2 : 1
D. a : b : c = 1 : 2 : 2
Cho hai hàm số F(x)
(
x
2
+
a
x
+
b
)
e
-
x
v
à
f
(
x
)
(
-
x
2
+
3
x
+
6
)
e
-
x
. Tìm a và b đ...
Đọc tiếp
Cho hai hàm số F(x)= ( x 2 + a x + b ) e - x v à f ( x ) = ( - x 2 + 3 x + 6 ) e - x . Tìm a và b để F(x) là một nguyên hàm của hàm số f(x)
A. a=1;b= -7
B. a= -1;b= -7
C. a= -1;b=7
D. a=1;b=7
Cho hàm số f(x) liên tục trên (1;e) thỏa mãn
x
f
x
−
f
1
+
ln
x
x
2
+
x
−
2
−
ln
x
. Biết rằng
∫
2
e
f
x
d
x
a
e...
Đọc tiếp
Cho hàm số f(x) liên tục trên (1;e) thỏa mãn x f x − f 1 + ln x = x 2 + x − 2 − ln x . Biết rằng ∫ 2 e f x d x = a e 2 + b e + c với a , b , c ∈ Q . Tính giá trị của T = a + b + c.
A. T = 11 2 .
B. T = -4
C. T = − 5 2 .
D. T = 3