Các câu hỏi tương tự
Một cái th ng đựng nước được tạo thành từ việc cắt mặt xung quanh của một hình nón bởi một mặt phẳng vuông góc với trục của hình nón. Miệng thùng là đường tròn có bán kính bằng hai lần bán kính mặt đáy của th ng. Bên trong thùng có một cái phễu dạng hình nón có đáy là đáy của th ng, có đ nh là tâm của miệng thùng và có chiều cao bằng 20cm (xem hình minh họa). Biết rằng đổ 4.000
c
m
3
nước vào th ng thì đầy th ng (nước không chảy được vào bên t...
Đọc tiếp
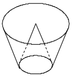
Một cái th ng đựng nước được tạo thành từ việc cắt mặt xung quanh của một hình nón bởi một mặt phẳng vuông góc với trục của hình nón. Miệng thùng là đường tròn có bán kính bằng hai lần bán kính mặt đáy của th ng. Bên trong thùng có một cái phễu dạng hình nón có đáy là đáy của th ng, có đ nh là tâm của miệng thùng và có chiều cao bằng 20cm (xem hình minh họa). Biết rằng đổ 4.000 c m 3 nước vào th ng thì đầy th ng (nước không chảy được vào bên trong phễu), tính bán kính đáy r của phễu (giá trị gần đúng của r làm tròn đến hàng phần trăm).
A. r = 9,77 cm
B. r = 7,98 cm
C. r = 5,64 cm
D. r = 5,22 cm
Từ một tấm tôn hình chữ nhật người ta cuộn thành một chiếc thùng hình trụ không đáy (như hình vẽ). Biết tấm tôn có chu vi bằng 120 cm. Để chiếc thùng có thể tích lớn nhất thì chiều dài, chiều rộng của tấm tôn lần lượt là A. 35 cm; 25 cm B. 30 cm; 30 cm C. 40 cm; 20 cm D. 50 cm; 10 cm
Đọc tiếp
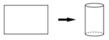
Từ một tấm tôn hình chữ nhật người ta cuộn thành một chiếc thùng hình trụ không đáy (như hình vẽ). Biết tấm tôn có chu vi bằng 120 cm. Để chiếc thùng có thể tích lớn nhất thì chiều dài, chiều rộng của tấm tôn lần lượt là
A. 35 cm; 25 cm
B. 30 cm; 30 cm
C. 40 cm; 20 cm
D. 50 cm; 10 cm
Một thùng đựng bia hơi (có dạng khối tròn xoay như hình vẽ) có đường kính đáy là 30 cm, đường kính lớn nhất của thân thùng là 40 cm, chiều cao thùng là 60 cm, các cạnh bên hông của thùng có hình dạng của một parabol. Thể tích của thùng bia hơi gần nhất với kết quả nào dưới đây? (giả sử độ dày thùng bia không đáng kể) A. 70 (lít). B. 62 (lít). C. 60 (lít). D. 64 (lít).
Đọc tiếp
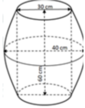
Một thùng đựng bia hơi (có dạng khối tròn xoay như hình vẽ) có đường kính đáy là 30 cm, đường kính lớn nhất của thân thùng là 40 cm, chiều cao thùng là 60 cm, các cạnh bên hông của thùng có hình dạng của một parabol. Thể tích của thùng bia hơi gần nhất với kết quả nào dưới đây? (giả sử độ dày thùng bia không đáng kể)
A. 70 (lít).
B. 62 (lít).
C. 60 (lít).
D. 64 (lít).
Hai cái thùng hình tròn có tỉ số là 1,5 . Tổng khối lượng của hai đáy là 1,3kg . Tính khối lượng mỗi đáy thùng .![]() Giải chi tiết hộ mk nha
Giải chi tiết hộ mk nha
Thu có một sợi dây dài 6,25m. Em quấn sợi dây quanh miệng cái chum hình tròn thì vừa đúng 5 vòng. Tính diện tích miệng cái chum đó.
Người ta sử dụng xe bồn để chở dầu. Thùng đựng dầu có thiết diện ngang (mặt trong của thùng) là một đường elip có độ dài trục lớn bằng 2m , độ dài trục bé bằng 1, 6m , chiều dài (mặt trong của thùng) bằng 3, 5m . Thùng được đặt sao cho trục bé nằm theo phương thẳng đứng (như hình bên). Biết chiều cao của dầu hiện có trong thùng (tính từ điểm thấp nhất của đáy thùng đến mặt dầu) là 1, 2m . Tính thể tích V của dầu có trong thùng (Kết quả làm tròn đến hàng phần trăm). A.
V...
Đọc tiếp
Người ta sử dụng xe bồn để chở dầu. Thùng đựng dầu có thiết diện ngang (mặt trong của thùng) là một đường elip có độ dài trục lớn bằng 2m , độ dài trục bé bằng 1, 6m , chiều dài (mặt trong của thùng) bằng 3, 5m . Thùng được đặt sao cho trục bé nằm theo phương thẳng đứng (như hình bên). Biết chiều cao của dầu hiện có trong thùng (tính từ điểm thấp nhất của đáy thùng đến mặt dầu) là 1, 2m . Tính thể tích V của dầu có trong thùng (Kết quả làm tròn đến hàng phần trăm).

A. V = 4 , 42 m 3
B. V = 2 , 02 m 3
C. V = 7 , 08 m 3
D. V = 2 , 31 m 3
Một người thợ thủ công cần làm một cái thùng hình hộp đứng không nắp đáy là hình vuông có thể tích 100
c
m
3
. Để tiết kiệm vật liệu làm thùng, người đó cần thiết kế sao cho tổng S của diện tích xung quanh và diện tích mặt đáy là nhỏ nhất A.
S
30
40
3
B.
S
40
40...
Đọc tiếp
Một người thợ thủ công cần làm một cái thùng hình hộp đứng không nắp đáy là hình vuông có thể tích 100 c m 3 . Để tiết kiệm vật liệu làm thùng, người đó cần thiết kế sao cho tổng S của diện tích xung quanh và diện tích mặt đáy là nhỏ nhất
A. S = 30 40 3
B. S = 40 40 3
C. S = 10 40 3
D. S = 20 40 3
Một người bán gạo muốn đóng một thùng tôn đựng gạo có thể tích không đổi bằng
8
m
3
, thùng tôn hình hộp chữ nhật có đáy là hình vuông, không nắp. Trên thị trường, giá tôn làm đáy thùng là
100.000
/
m
2
và giá tôn làm thành xung quanh thùng là
50.000
/
m
2
. Hỏi người bán gạo đó cần đóng thùng đựng gạo với cạnh đáy bằng bao n...
Đọc tiếp
Một người bán gạo muốn đóng một thùng tôn đựng gạo có thể tích không đổi bằng 8 m 3 , thùng tôn hình hộp chữ nhật có đáy là hình vuông, không nắp. Trên thị trường, giá tôn làm đáy thùng là 100.000 / m 2 và giá tôn làm thành xung quanh thùng là 50.000 / m 2 . Hỏi người bán gạo đó cần đóng thùng đựng gạo với cạnh đáy bằng bao nhiêu để chi phí mua nguyên liệu là nhỏ nhất ?
<!-- MathType@Translator@5@5@MathML3 (namespace attr).tdl@MathML 3.0 (namespace attr)@ -->
<math display='block' xmlns='http://www.w3.org/1998/Math/MathML'>
<semantics>
<mrow>
<mn>50.000</mn><mo>/</mo><msup>
<mi>m</mi>
<mn>2</mn>
</msup>
</mrow>
<annotation encoding='MathType-MTEF'>MathType@MTEF@5@5@+=
feaahqart1ev3aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn
hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr
4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq=Jc9
vqaqpepm0xbba9pwe9Q8fs0=yqaqpepae9pg0FirpepeKkFr0xfr=x
fr=xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaGynaiaaic
dacaGGUaGaaGimaiaaicdacaaIWaGaai4laiaad2gadaahaaWcbeqa
aiaaikdaaaaaaa@3CDA@
</annotation>
</semantics>
</math>
<!-- MathType@End@5@5@ -->
B. 1,5m
C. 2m
A. 1m
Từ một tấm tôn hình chữ nhật kích thước 50cm x 240cm, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây):* Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.* Cách 2: Cắt tấm tôn ban đầu thành hai tấm tôn bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng. Kí hiệu
V
1
là thể tích của thùng gò được theo cách 1 và
V
2
là tổng thể tích của hai thùn...
Đọc tiếp
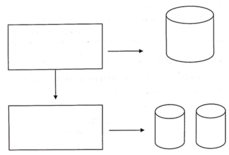
Từ một tấm tôn hình chữ nhật kích thước 50cm x 240cm, người ta làm các thùng đựng nước hình trụ có chiều cao bằng 50cm, theo hai cách sau (xem hình minh họa dưới đây):
* Cách 1: Gò tấm tôn ban đầu thành mặt xung quanh của thùng.
* Cách 2: Cắt tấm tôn ban đầu thành hai tấm tôn bằng nhau, rồi gò mỗi tấm đó thành mặt xung quanh của một thùng. Kí hiệu V 1 là thể tích của thùng gò được theo cách 1 và V 2 là tổng thể tích của hai thùng gò được theo cách 2. Tính tỉ số V 1 V 2
A. V 1 V 2 = 1 2
B. V 1 V 2 = 1
C. V 1 V 2 = 2
D. V 1 V 2 = 2







