\(l=\sqrt{R^2+h^2}=R\sqrt{2}\)
\(S_{xq}=2\cdot\Omega\cdot R\cdot l\)
=>\(2\cdot\Omega\cdot R\cdot R\sqrt{2}=18\)
=>\(R^2=\dfrac{18}{2\Omega\sqrt{2}}=\dfrac{9}{\Omega\sqrt{2}}\)
=>\(R=\dfrac{3}{\sqrt{\Omega\sqrt{2}}}\left(cm\right)\)
\(l=\sqrt{R^2+h^2}=R\sqrt{2}\)
\(S_{xq}=2\cdot\Omega\cdot R\cdot l\)
=>\(2\cdot\Omega\cdot R\cdot R\sqrt{2}=18\)
=>\(R^2=\dfrac{18}{2\Omega\sqrt{2}}=\dfrac{9}{\Omega\sqrt{2}}\)
=>\(R=\dfrac{3}{\sqrt{\Omega\sqrt{2}}}\left(cm\right)\)
Cho hình trụ có bán kính đáy R = 4 (cm) và chiều cao h = 5 (cm). Diện tích xung quanh của hình trụ là:
A. 40 π
B. 30 π
C. 20 π
D. 50 π
Cho hình trụ có bán kính đáy R = 4 (cm) và chiều cao h = 5 (cm). Diện tích xung quanh của hình trụ là:
A. 40 π
B. 30 π
C. 20 π
D. 50 π
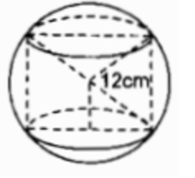
Một hình trụ được “đặt khít” vào bên trong một hình cầu bán kính r = 12cm như hình 112. Hãy tính: Diện tích xung quanh của hình trụ, biết chiều cao của hình trụ bằng đường kính đáy của nó.
Một hình trụ có bán kính đáy là 5cm, diện tích xung quanh bằng 300 π ( c m 2 ). Chiều cao của hình trụ là?
A. 6cm
B. 12cm
C. 30cm
D. 10cm
Một hình trụ có bán kính đáy là 7cm, diện tích xung quanh bằng 352 c m 2 . Khi đó chiều cao của hình trụ gần bằng là:
Một hình trụ có chiều cao bằng đường kính đáy . Diện tích xung quanh của hình trụ đó bằng bao nhiêu nếu bán kính đáy bằng 6 cm
Một hình trụ có chiều cao bằng đường kính đáy. Biết bán kính đáy bằng 6 m và tính diện tích xung quanh hình trụ
Một hình trụ có bán kính đáy là 3cm. Biết diện tích toàn phần của hình trụ gấp đôi diện tích xung quanh. Tính chiều cao của hình trụ
Chiều cao của 1 hình trụ bằng bán kính đường tròn đáy. Diện tích xung quanh của hình trụ là 628 c m 2 . Tính thể tích hình trụ.
A. 1000 π
B. 100 π
C. 500 π
D.Đáp án khác
Cho hình trụ có bán kính đường tròn đáy r=2cm và chiều cao h=5cm. Tính diện tích xung quanh hình trụ đó