Các câu hỏi tương tự
Một hình trụ có độ dài đường cao gấp đôi đường kính đáy. Biết thể tích của hình trụ là 128π c m 3 . Tính diện tích xung quanh của hình trụ
Một vật thể dạng hình trụ bán kính đường tròn đáy và độ dài của nó đều bằng 2r (cm). Người ta khoan một lỗ cũng có dạng hình trụ như hình sau, có bán kính đáy và độ sâu đều bằng r(cm) .Thể tích phần vật thể còn lại (tính theo
c
m
3
) là:A.4π
r
3
B.7π
r
3
C.8π...
Đọc tiếp
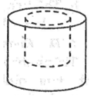
Một vật thể dạng hình trụ bán kính đường tròn đáy và độ dài của nó đều bằng 2r (cm). Người ta khoan một lỗ cũng có dạng hình trụ như hình sau, có bán kính đáy và độ sâu đều bằng r(cm) .Thể tích phần vật thể còn lại (tính theo c m 3 ) là:
A.4π r 3 B.7π r 3 C.8π r 3 D.9π r 3
Một hình nón có bán kính đáy là R,diện tích xung quanh bằng hai lần diện tích đáy của nó.Khi đó thể tích hình nón bằng
A.\(\dfrac{\pi R^3\sqrt{3}}{3}\)cm3 B.\(\pi R^3\sqrt{3}\)cm3 C.\(\dfrac{\pi R^3\sqrt{5}}{3}\)cm3 D.\(\dfrac{\pi R^3\sqrt{5}}{5}\)cm3
Một hình trụ có đường cao bằng đường kính đáy. Biết rằng thể tích hình trụ là 128 π c m 3 . Tính diện tích xung quanh của nó.
Một hình cầu đặt vừa khít vào trong một hình trụ như hình bên (chiều cao của hình trụ bằng độ dài đường kính của hình cầu) thì thể tích của nó bằng 2/3 thể tích của hình trụ.Nếu đường kính của hình cầu là d (cm) thì thể tích của hình trụ là:A. (1/4).
πd
3
cm
3
B. (1/3).
πd
3
cm...
Đọc tiếp
Một hình cầu đặt vừa khít vào trong một hình trụ như hình bên (chiều cao của hình trụ bằng độ dài đường kính của hình cầu) thì thể tích của nó bằng 2/3 thể tích của hình trụ.
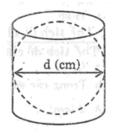
Nếu đường kính của hình cầu là d (cm) thì thể tích của hình trụ là:
A. (1/4). πd 3 cm 3 B. (1/3). πd 3 cm 3
C.(2/3). πd 3 cm 3 D. (3/4). πd 3 cm 3
Một hình trụ có bán kính đáy 1cm và chiều cao 2cm người ta khoan đi một phần có dạng hình nón như hình vẽ thì phần thể tích còn lại của nó sẽ là :
A
.
2
π
3
(
c
m
3
)
...
Đọc tiếp
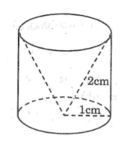
Một hình trụ có bán kính đáy 1cm và chiều cao 2cm người ta khoan đi một phần có dạng hình nón như hình vẽ thì phần thể tích còn lại của nó sẽ là :
 A
.
2
π
3
(
c
m
3
)
B
.
4
π
3
(
c
m
3
)
C
.
2
π
(
c
m
3
)
D
.
8
π
3
(
c
m
3
)
A
.
2
π
3
(
c
m
3
)
B
.
4
π
3
(
c
m
3
)
C
.
2
π
(
c
m
3
)
D
.
8
π
3
(
c
m
3
)
Một hình trụ có bán kính đáy là 3cm. Biết diện tích toàn phần của hình trụ gấp đôi diện tích xung quanh. Tính chiều cao của hình trụ
một hình chữ nhật có chiều dài gấp hai lần chiều rộng, quay hình chữ nhật đó một vòng quanh chiều dài cố định ta được một hình trụ có diện tích xung quanh bằng 100 cm2.
a.Tính bán kính đáy r và chiều cao h của hình trụ.
b.Tính diện tích toàn phần và thể tích hình trụ
Một hình trụ có bán kính đáy R = 3 cm và độ dài đường sinh bằng 2 cm. Biết diện tích xung quanh bằng thể tích hình trụ. Tính thể tích hình trụ






