Các câu hỏi tương tự
Hình bên là hình nón .chiều cao là h(cm),bán kính đường tròn đáy là r(cm) và độ dài đường sinh là m(cm) thì thể tích hình nón này là:A.
π
.
r
2
h (
c
m
3
) B. (1/3)
π
.
r
2
h (
c
m...
Đọc tiếp
Hình bên là hình nón .chiều cao là h(cm),bán kính đường tròn đáy là r(cm) và độ dài đường sinh là m(cm) thì thể tích hình nón này là:
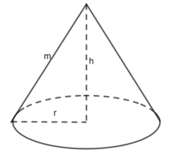
A. π . r 2 h ( c m 3 ) B. (1/3) π . r 2 h ( c m 3 )
C. π .r.m ( c m 3 ) D. π r(r+m) ( c m 3 )
Với nửa hình cầu bán kính r và một hình trụ có bán kính đường tròn đáy và chiều cao đều bằng h. Khi h = 12 (cm) và tổng diện tích nửa mặt cầu và diện tích “hình tròn đáy” gấp ba lần diện tích toàn phần của hình trụ thì r (cm) bằng bao nhiêu?
Với một hình nón có bán kính đường tròn đáy là r (cm) và chiều cao 2r (cm) và một hình cầu bán kính r (cm). Hãy tính:Thể tích hình nón, biết thể tích hình cầu là 15,8
c
m
3
Đọc tiếp
Với một hình nón có bán kính đường tròn đáy là r (cm) và chiều cao 2r (cm) và một hình cầu bán kính r (cm). Hãy tính:
Thể tích hình nón, biết thể tích hình cầu là 15,8 c m 3
Cho một hình nón có bán kính đường tròn đáy là r (cm), chiều cao 2r (cm) và một hình cầu có bán kính r (cm). Hãy tính:a, Diện tích mặt cầu, biết diện tích toàn phần của hình nón là 21,06
c
m
2
b, Thể tích của hình nón, biết thể tích của hình cầu là 15,8
c
m
3
Đọc tiếp
Cho một hình nón có bán kính đường tròn đáy là r (cm), chiều cao 2r (cm) và một hình cầu có bán kính r (cm). Hãy tính:
a, Diện tích mặt cầu, biết diện tích toàn phần của hình nón là 21,06 c m 2
b, Thể tích của hình nón, biết thể tích của hình cầu là 15,8 c m 3
Với một hình nón có bán kính đường tròn đáy là r (cm) và chiều cao 2r (cm) và một hình cầu bán kính r (cm). Hãy tính:Diện tích mặt cầu, biết diện tích toàn phần của hình nón là 21,06
c
m
2
Đọc tiếp
Với một hình nón có bán kính đường tròn đáy là r (cm) và chiều cao 2r (cm) và một hình cầu bán kính r (cm). Hãy tính:
Diện tích mặt cầu, biết diện tích toàn phần của hình nón là 21,06 c m 2
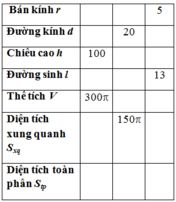
Cho hình nón có bán kính đáy r, đường kính đáy d, chiều cao h, đường sinh l, thể tích V, diện tích xung quanh Sxq, diện tích toàn pphần Stp. Điền các kết quả vào ô trống trong bảng sau:
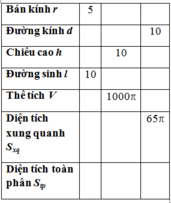
Cho hình nón có bán kính đáy r, đường kính đáy d, chiều cao h, đường sinh l, thể tích V, diện tích xung quanh Sxq, diện tích toàn phần Stp. Điền các kết quả vào ô trống trong bảng sau:
Cho đường tròn tâm O bán kính r và đường thẳng d không có điểm chung với r. từ điểm b thuộc đường thẳng d kẻ hai tiếp tuyến PA PB đường tròn tâm O .Vẽ đường kính BC. Gọi H là hình chiếu của A trên BC.
a) cm tu giac PAOB noi tiep .
b) cho OP=2R tinh độ dài cung nhỏ AB theo R
Cho đường tròn tâm O, bán kính R. Đường thẳng d tiếp xúc với đường tròn (O;R) tại A. Trên đường thẳng d lấy điểm H sao cho AHR. Qua H kể đường thẳng vuông góc với dường thẳng d, cắt (O;R) tại 2 điể E và B (E nằm giữa B và H ).a, CMR: Góc ABE bằng góc EAH.b, Trên đường thẳng d lấy điểm C sao cho H là trung điểm của đoạn AC. Đường thẳng CE cắt AB tại K. CMR tứ giác AHEK nội tiếp được đường tròn.c, Xác định vị trí của H trên đường thẳng D sao cho ABR√3
Đọc tiếp
Cho đường tròn tâm O, bán kính R. Đường thẳng d tiếp xúc với đường tròn (O;R) tại A. Trên đường thẳng d lấy điểm H sao cho AH<R. Qua H kể đường thẳng vuông góc với dường thẳng d, cắt (O;R) tại 2 điể E và B (E nằm giữa B và H ).
a, CMR: Góc ABE bằng góc EAH.
b, Trên đường thẳng d lấy điểm C sao cho H là trung điểm của đoạn AC. Đường thẳng CE cắt AB tại K. CMR tứ giác AHEK nội tiếp được đường tròn.
c, Xác định vị trí của H trên đường thẳng D sao cho AB=R√3