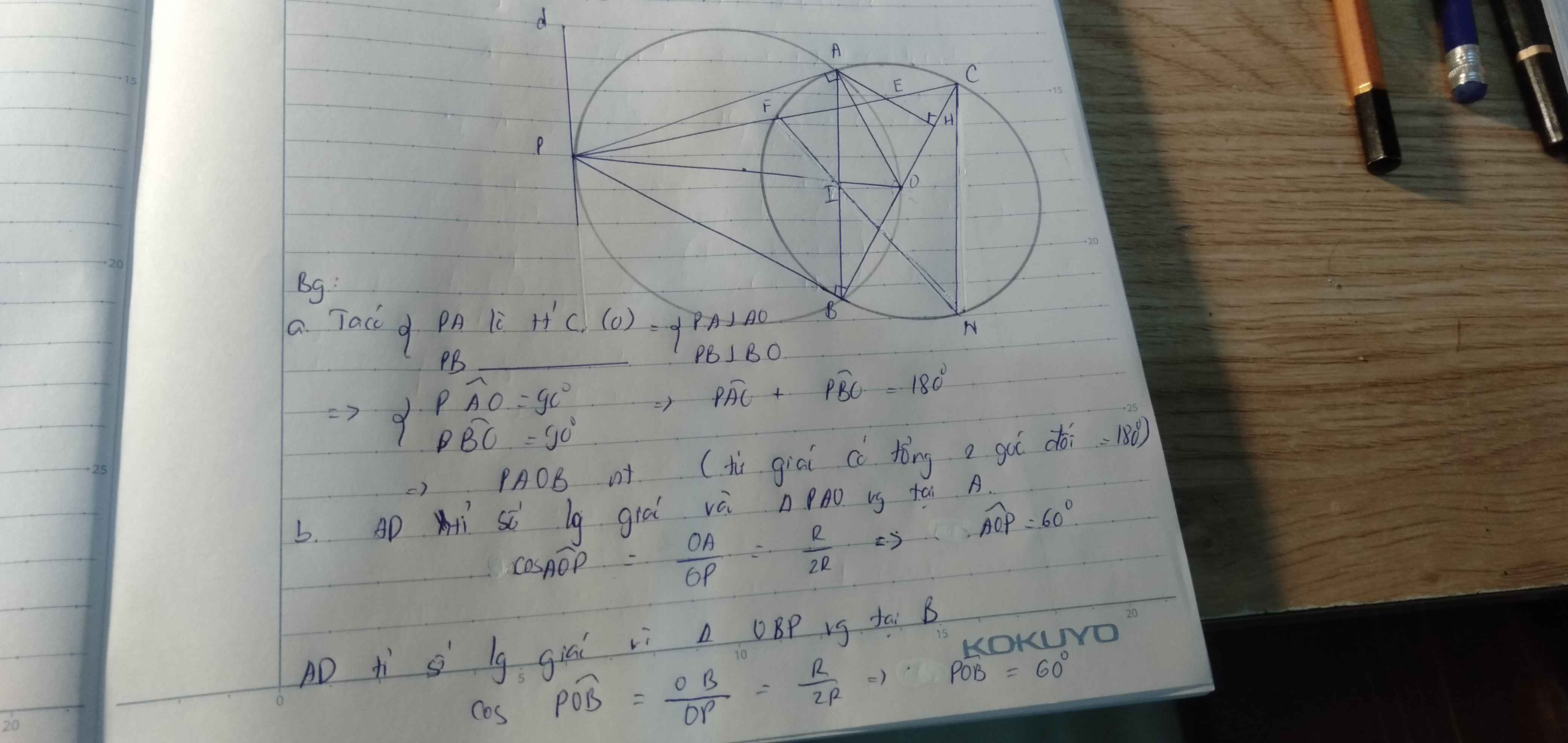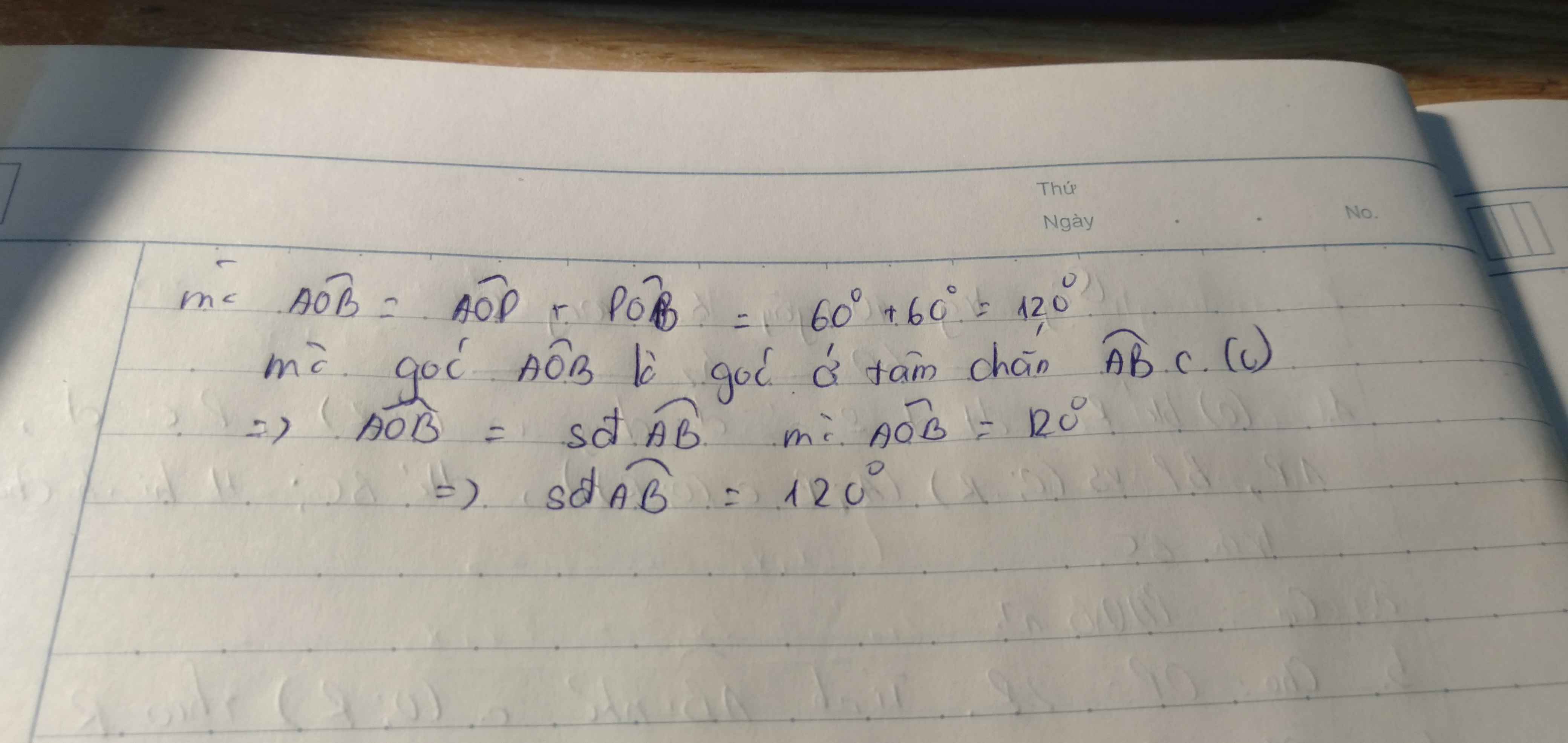Các câu hỏi tương tự
Cho đường tròn tâm O, bán kính R. Điểm A thuộc đường tròn, BC là một đường kính (A khác B và C) . Vẽ AH vuông góc với BC tại H. Gọi E, M lần lượt là trung điểm của AB, AH và P là giao điểm của OE với tiếp tuyến tại A của (O ; R).a) CMR: AB2 BH.BC b) CM: PB là tiếp tuyến của đường tròn (O)c) CM: 3 điểm P, M, C thẳng hàngd) Gọi Q là giao điểm của đường thẳng PA với tiếp tuyến tại C của đường tròn (O). Khi A thay đổi trên đường tròn (O), tìm giá trị nhỏ nhất của tổng OP + OQ
Đọc tiếp
Cho đường tròn tâm O, bán kính R. Điểm A thuộc đường tròn, BC là một đường kính (A khác B và C) . Vẽ AH vuông góc với BC tại H. Gọi E, M lần lượt là trung điểm của AB, AH và P là giao điểm của OE với tiếp tuyến tại A của (O ; R).
a) CMR: AB2 = BH.BC
b) CM: PB là tiếp tuyến của đường tròn (O)
c) CM: 3 điểm P, M, C thẳng hàng
d) Gọi Q là giao điểm của đường thẳng PA với tiếp tuyến tại C của đường tròn (O). Khi A thay đổi trên đường tròn (O), tìm giá trị nhỏ nhất của tổng OP + OQ
Cho đường tròn tâm O, bán kính R. Điểm A thuộc đường tròn, BC là một đường kính (A khác B và C) . Vẽ AH vuông góc với BC tại H. Gọi E, M lần lượt là trung điểm của AB, AH và P là giao điểm của OE với tiếp tuyến tại A của (O ; R).a) CMR: AB2 BH.BC b) CM: PB là tiếp tuyến của đường tròn (O)c) CM: 3 điểm P, M, C thẳng hàngd) Gọi Q là giao điểm của đường thẳng PA với tiếp tuyến tại C của đường tròn (O). Khi A thay đổi trên đường tròn (O), tìm giá trị nhỏ nhất của tổng OP + OQ
Đọc tiếp
Cho đường tròn tâm O, bán kính R. Điểm A thuộc đường tròn, BC là một đường kính (A khác B và C) . Vẽ AH vuông góc với BC tại H. Gọi E, M lần lượt là trung điểm của AB, AH và P là giao điểm của OE với tiếp tuyến tại A của (O ; R).
a) CMR: AB2 = BH.BC
b) CM: PB là tiếp tuyến của đường tròn (O)
c) CM: 3 điểm P, M, C thẳng hàng
d) Gọi Q là giao điểm của đường thẳng PA với tiếp tuyến tại C của đường tròn (O). Khi A thay đổi trên đường tròn (O), tìm giá trị nhỏ nhất của tổng OP + OQ
Cho (O;R). Từ điểm P nằm ngoài đường tròn kẻ các tiếp tuyến PA, PB (A, B là 2 tiếp điểm) và kẻ đường kính AC của đường tròn
a) C/m PAOB nội tiếp
b) C/m PO // BC. Cho OP = 2R. Tính góc AOB và diện tích hình quạt tròn AOB (ứng với cung nhỏ AB)
Cho đường tròn tâm O, bán kính R và một điểm A sao cho OA2R. VẼ các tiếp tuyến AB,AC ( B,C) là các tiếp điểm. Đường thẳng OA cắt BC tại H, cắt cung nhỏ BC và cung lớn BC lần lượt tại I,Ka/ CM OA vuông góc với BC, HIOAR bình phươngb/ CM tam gaics ABC đều, tứ giác ABKC là hình thoic/ CHứng tỏ I là tâm đường tròn nội tiếp tam giác ABC. Tính theo R bán kính của đường tròn này. d/ Vẽ cát tueyens bất kì AMN của đường tròn tâm O. Gọi E là tủng điểm MN. CHứng tỏ 5 điểm O,E,A,B,C cùng thuộc một đường tr...
Đọc tiếp
Cho đường tròn tâm O, bán kính R và một điểm A sao cho OA=2R. VẼ các tiếp tuyến AB,AC ( B,C) là các tiếp điểm. Đường thẳng OA cắt BC tại H, cắt cung nhỏ BC và cung lớn BC lần lượt tại I,K
a/ CM OA vuông góc với BC, HI=OA=R bình phương
b/ CM tam gaics ABC đều, tứ giác ABKC là hình thoi
c/ CHứng tỏ I là tâm đường tròn nội tiếp tam giác ABC. Tính theo R bán kính của đường tròn này.
d/ Vẽ cát tueyens bất kì AMN của đường tròn tâm O. Gọi E là tủng điểm MN. CHứng tỏ 5 điểm O,E,A,B,C cùng thuộc một đường tròn
Cho đường tròn (O;R) đường kính AB. Trên tiếp tuyến tại A của (O;R) lấy điểm C sao cho AC 2R. Gọi D là giao điểm của BC và đường tròn (O)a) CM: AD là đường cao và cũng là đường trung tuyến của ΔABCb) Vẽ dây cung AE vuông góc với OC tại H. CM:CE là tiếp tuyến của đường tròn (O;R)c) Đường thẳng BE cắt đường thẳng OD tại F. Tính tanOBF và suy ra số độ của góc OFBd) Gọi K là hình chiếu của điểm E xuống AB, M là giao điểm của EK với BC. Tính độ dài các đoạn thẳng ME và MK theo R
Đọc tiếp
Cho đường tròn (O;R) đường kính AB. Trên tiếp tuyến tại A của (O;R) lấy điểm C sao cho AC = 2R. Gọi D là giao điểm của BC và đường tròn (O)
a) CM: AD là đường cao và cũng là đường trung tuyến của ΔABC
b) Vẽ dây cung AE vuông góc với OC tại H. CM:CE là tiếp tuyến của đường tròn (O;R)
c) Đường thẳng BE cắt đường thẳng OD tại F. Tính tanOBF và suy ra số độ của góc OFB
d) Gọi K là hình chiếu của điểm E xuống AB, M là giao điểm của EK với BC. Tính độ dài các đoạn thẳng ME và MK theo R
Cho nửa đường tròn (O), đường kính AB2R. Lấy một điểm C trên nửa đường tròn sao cho góc ABC30 độ. Gọi P là giao điểm của tiếp tuyến tại A với nửa đường tròn đường thẳng BC.a) CM: tam giác ABC vuông và PA^2PB.PCb) Từ P vẽ tiếp tuyến thứ hai với đường tròn (O) tại M(M là tiếp điểm). CM: PO là đường trung trực của AMC)PO cắt AM tại N. Tính PA , PO , AM theo Rd) Vẽ MH vuông góc AB tại H. Gọi I là giao điểm của PB và MH. Tính NI theo R
Đọc tiếp
Cho nửa đường tròn (O), đường kính AB=2R. Lấy một điểm C trên nửa đường tròn sao cho góc ABC=30 độ. Gọi P là giao điểm của tiếp tuyến tại A với nửa đường tròn đường thẳng BC.
a) CM: tam giác ABC vuông và PA^2=PB.PC
b) Từ P vẽ tiếp tuyến thứ hai với đường tròn (O) tại M(M là tiếp điểm). CM: PO là đường trung trực của AM
C)PO cắt AM tại N. Tính PA , PO , AM theo R
d) Vẽ MH vuông góc AB tại H. Gọi I là giao điểm của PB và MH. Tính NI theo R
cho đường tròn tâm O bán kính R đường kính AB. Vẽ điểm C thuộc đường tròn tâm O bán kính R sao cho AC bằng R .kẻ OH vuông góc với AC tại H . qua điểm C vẽ một tiếp tuyến của đường tròn tâm O bán kính R tiếp tuyến này cắt đường thẳng OH tại D Câu a/ chứng minh AD là tiếp tuyến của đường tròn tâm O bán kính R Câu b/ tính BC theo R và tỉ số lượng giác của góc ABCCau c/ gọi M là điểm thuộc tia đối của tia CA . chứng minh MC nhân với MA bằng MO bình phương trừ AO bình phương
Đọc tiếp
cho đường tròn tâm O bán kính R đường kính AB. Vẽ điểm C thuộc đường tròn tâm O bán kính R sao cho AC bằng R .kẻ OH vuông góc với AC tại H . qua điểm C vẽ một tiếp tuyến của đường tròn tâm O bán kính R tiếp tuyến này cắt đường thẳng OH tại D
Câu a/ chứng minh AD là tiếp tuyến của đường tròn tâm O bán kính R
Câu b/ tính BC theo R và tỉ số lượng giác của góc ABC
Cau c/ gọi M là điểm thuộc tia đối của tia CA . chứng minh MC nhân với MA bằng MO bình phương trừ AO bình phương
Cho đường tròn tâm O bán kính R và một điểm M sao cho OM2R,từ M kẻ hai tiếp tuyến MA,MB của đường tròn tâm O bán kính R (A,B là tiếp điểm).a)Chứng minh tam giác MAB đều,tính AM theo Rb)Qua điểm C thuộc ucng nhỏ AB vẽ tiếp tuyến với đường tròn tâm O bán kính R cắt MA tại E,cắt MB tại F,OF cắt AB tại K,OE cắt AB tại H.Chứng minh EK vuống góc với OFc)Khi số đo cung BC90 độ.Tính EF và diện tích tam giác OHK theo R
Đọc tiếp
Cho đường tròn tâm O bán kính R và một điểm M sao cho OM=2R,từ M kẻ hai tiếp tuyến MA,MB của đường tròn tâm O bán kính R (A,B là tiếp điểm).
a)Chứng minh tam giác MAB đều,tính AM theo R
b)Qua điểm C thuộc ucng nhỏ AB vẽ tiếp tuyến với đường tròn tâm O bán kính R cắt MA tại E,cắt MB tại F,OF cắt AB tại K,OE cắt AB tại H.Chứng minh EK vuống góc với OF
c)Khi số đo cung BC=90 độ.Tính EF và diện tích tam giác OHK theo R
cho đường tròn tâm O bán kính r , điểm A nằm ngoài đường tròn tâm O . vẽ tiếp tuyến AB của đướng tròn tâm O , vẽ dây cung BC của đường tròn tâm O vuông góc với OA tại H a, Cm H là trung điểmcủa BC b, CM AC là tiếp tuyến của đường tròn tâm O c, OA 2r cm tam giác ABC đềud, trên tia dối của tia BC lấy Q ,từ Q kẻ 2 tiếp tuyến QD và QE của đường tròn tâm O .CM AED thẳng hàng
Đọc tiếp
cho đường tròn tâm O bán kính r , điểm A nằm ngoài đường tròn tâm O . vẽ tiếp tuyến AB của đướng tròn tâm O , vẽ dây cung BC của đường tròn tâm O vuông góc với OA tại H
a, Cm H là trung điểmcủa BC
b, CM AC là tiếp tuyến của đường tròn tâm O
c, OA = 2r cm tam giác ABC đều
d, trên tia dối của tia BC lấy Q ,từ Q kẻ 2 tiếp tuyến QD và QE của đường tròn tâm O .CM AED thẳng hàng