Chọn B.
Phương pháp:
Sử dụng lý thuyết khối đa diện để là bài toán.
Cách giải:
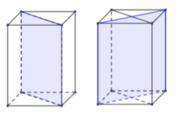
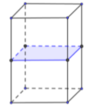
Hình đã cho có 3 mặt phẳng đối xứng.
Chọn B.
Phương pháp:
Sử dụng lý thuyết khối đa diện để là bài toán.
Cách giải:


Hình đã cho có 3 mặt phẳng đối xứng.
Hình hộp đứng có đáy hình thoi (không phải hình vuông) có bao nhiêu mặt phẳng đối xứng?
A. Bốn.
B. Năm.
C. Sáu.
D. Ba.
Hình hộp đứng đáy là hình thoi có bao nhiêu mặt phẳng đối xứng?
A. 1
B. 2
C. 3
D. 4
Hình hộp đứng đáy là hình thoi có bao nhiêu mặt phẳng đối xứng?
A. 3.
B. 2.
C. 4.
D. 1
Hình hộp đứng đáy là hình thoi có bao nhiêu mặt phẳng đối xứng
A. 1
B. 3
C. 4
D. 2
Lăng trụ đứng có đáy là hình thoi có bao nhiêu mặt phẳng đối xứng?
A. 9
B. 2
C. 5
D. 3
Số mặt phẳng đối xứng của hình hộp đứng có đáy là hình vuông là:
A. 3.
B. 4.
C. 6.
D. 5.
Hình hộp chữ nhật chỉ có hai đáy là hai hình vuông có tất cả bao nhiêu mặt phẳng đối xứng?
A. 4
B. 3
C. 9
D. 5
Một hình hộp chữ nhật (không phải hình lập phương) có bao nhiêu mặt phẳng đối xứng?
A.4
B.2
C.0
D.1
Số mặt phẳng đối xứng của hình lăng trụ đứng có đáy là hình vuông là:
A. 3
B. 1
C. 5
D. 4