Đáp án A
Chiều cao của cánh cửa cũng là chiều cao của buồng cửa hình trụ. Chiều rộng của cánh cửa chính là bán kính đáy của buồng cửa hình trụ. Theo công thức thể tích hình trụ, ta có thể tích của buồng cửa
Một cửa hàng có 100 quả cam, một người muốn xếp 100 quả cam thành một tứ diện có 4 mặt, mỗi mặt là hình tam giác và đáy là hình vuông (như hình vẽ).
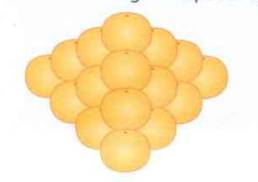
Biết số quả cam trong khối tứ diện bốn mặt với n lớp được tính theo công thức \(\dfrac{1}{6}n\left(n+1\right)\left(n+2\right)\). Tính số lớp tối đa người này có thể xếp 100 quả cam thành hình tứ diện như trên.
Học sinh A thiết kế bảng điều khiển điện tử mở cửa phòng học của lớp mình. Bảng gồm 10 nút, mỗi nút được ghi một số từ 0 đến 9 và không có hai nút nào được ghi cùng một số. Để mở cửa cần nhấn liên tiếp 3 nút khác nhau sau cho 3 số trên nút đó theo thứ tự đã nhấn tạo thành một dãy số tăng và có tổng bằng 10. Học sinh B không biết quy tắc mở cửa trên, đã nhấn ngẫu nhiên liên tiếp 3 nút khác nhau trên bảng điều khiển. Tính xác xuất để B mở được cửa phòng học đó.
Trong không gian, cho hình chữ nhật ABCD có AB= 1 và AD = 2. Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ (tham khảo hình vẽ bên). Tính diện tích toàn phần S t p của hình trụ đó.
A. S t p = 4 π 3
B. S t p = 3 π
C. S t p = 4 π
D. S t p = 6 π
Cho một chiếc cốc thủy tinh có hình lăng trụ lục giác đều có chiều cao và độ dài cạnh đáy lần lượt là 20 cm và 5 cm. Người ta đặt cái cốc vào trong một hộp có dạng hình hộp chữ nhật sao cho cái cốc vừa khít trong hộp. Tính thể tích chiếc hộp đó.
A . 500 3 cm3
B . 1000 3 cm3
C . 750 3 cm3
D . 100 3 cm3
Một cái bồn gồm hai nửa hình cầu đường kính 18dm và một hình trụ có chiều cao 36dm (như hình vẽ). Tính thể tích V của cái bồn đó
A. V = 9216 π dm 3
B. V = 1024 π 9 d m 3
C. V = 16 π 243 d m 3
D. V = 3888 d m 3
Trong không gian, cho hình chữ nhật ABCD có AB = 2, AD = 3. Đường thẳng d nằm trong mặt phẳng (ABCD), không có điểm chung với ABCD, song song với cạnh AB và cách AB một khoảng bằng 1. Tính thể tích V của khối tròn xoay, nhận được khi quay hình chữ nhật ABCD quanh trục d.
A. V = 17 π
B. V = 5 π
C. V = 15 π
D. 30 π
Hình chữ nhật ABCD có AB = 4, AD = 2. Gọi M và N lần lượt là trung điểm của AB và CD. Cho hình chữ nhật quay quanh MN ta được một khối tròn xoay có thể tích V bằng
Trong không gian, cho hình chữ nhật ABCD có AB=1 và AD=2 Gọi M, N lần lượt là trung điểm của AD và BC. Quay hình chữ nhật đó xung quanh trục MN, ta được một hình trụ. Tính diện tích toàn phần S t p của hình trụ đó.
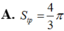
Công ty X thiết kế bảng điều khiển điện tử để mở hoặc khóa cửa một ngôi nhà. Bảng gồm 5 nút, mỗi nút được ghi một số từ 1 đến 5 và không có hai nút nào được ghi cùng một số. Để mở được cửa cần nhấn liên tiếp ít nhất 3 nút khác nhau sao cho tổng của các số trên các nút đó bằng 10. Một người không biết quy tắc mở cửa trên, đã nhấn ngẫu nhiên liên tiếp ít nhất 3 nút khác nhau trên bảng điều khiển. Xác suất P để người đó mở được cửa ngôi nhà là
A. P=0,17
B. P=0,7
C=0,12
D. 0,21
