Ta có thiết diện mặt cắt qua trục của chiếc ăng-ten là:
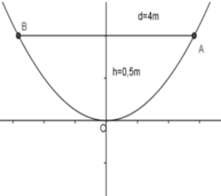
Vậy ta có: A(2; 1/2) mà A ∈ prapol:
![]()
Ta có thiết diện mặt cắt qua trục của chiếc ăng-ten là:

Vậy ta có: A(2; 1/2) mà A ∈ prapol:
![]()
mặt cắt của một chảo ăng ten là một phần của parabol cho biết đầu thu tín hiệu đặt tại tiêu điểm F cách đỉnh O của chảo một khoảng là 20 cm. Tính độ dài đường kính của chảo parabol trên biết khoảng cách từ một điểm bất kì trên miệng chảo đến đỉnh của chảo là 40 cm
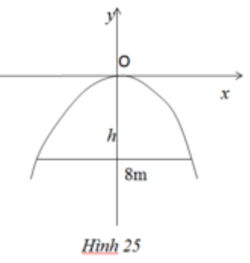
Một chiếc cổng hình parabol dạng y = - x 2 / 2 có chiều rộng d = 8m. Hãy tính chiều cao h của cổng (h.25).
Câu 1: Cho parabol (P):y=x^2+bx+c (b,c là các tham số thực)
a. Tìm giá trị của b,c biết parabol (P) đi qua điểm M(-3;2) và có trục đối xứng là đường thẳng x=-1
b. Với giá trị của b,c tìm được ở câu a), tìm m để đường thẳng d:y=-x-m cắt parabol(P) tại 2 điểm phân biệt A,B sao cho tam giác OAB vuông tại O( với O là gốc toạ độ)
Xác định số parabol y= ax^2+ x+c biết parabol đi qua điểm A ( 2;4) và có trục đối xứng x= 1/2
Xác định parabol y = ax2 + bx + 2, biết rằng parabol đó: Đi qua hai điểm A(3; -4) và có trục đối xứng là x = -3/2
Xác định Parabol (P): y = ax 2 + b x − 5 biết rằng Parabol đi qua điểm A (3; -4)và có trục đối xứng x = - 3 2
A. y = 1 18 x 2 + 1 6 x − 5
B. y = 1 18 x 2 + 1 6 x + 5
C. y = 3 x 2 + 9 x − 9
D. y = − 1 18 x 2 + 1 6 x − 5
Xác định parabol y = 3x^2+bx+c, biết rằng parabol đó đi qua A(2;19) và nhận đường thẳng x = -2/3 làm trục đối xứng.
Cho parabol (P) = x2+5x+2 và đường thẳng (d) y= mx
a. Vẽ (P)và d trên cùng hệ trục tọa độ
b. Tìm điều kiện của m để d cắt (P) tại 2 điểm phân biệt sao cho một điểm có
hoành độ bằng 1