a: \(\text{Δ}=\left(-m\right)^2-4\cdot2\cdot\left(m-2\right)\)
\(=m^2-8m+16=\left(m-4\right)^2>=0\forall m\)
=>Phương trình luôn có nghiệm với mọi m
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{m}{2}\\x_1x_2=\dfrac{c}{a}=\dfrac{m-2}{2}\end{matrix}\right.\)
\(y_1+y_2=x_1+x_2\)
=>\(y_1+y_2=\dfrac{m}{2}\)
\(y_1^2+y_2^2=1\)
=>\(\left(y_1+y_2\right)^2-2y_1y_2=1\)
=>\(\left(\dfrac{m}{2}\right)^2-2y_1y_2=1\)
=>\(2y_1y_2=\dfrac{m^2}{4}-1=-\dfrac{3}{4}m^2\)
=>\(y_1y_2=-\dfrac{3}{8}m^2\)
Phương trình bậc hai cần tìm là:
\(A^2-\dfrac{m}{2}\cdot A-\dfrac{3}{8}m^2=0\)


















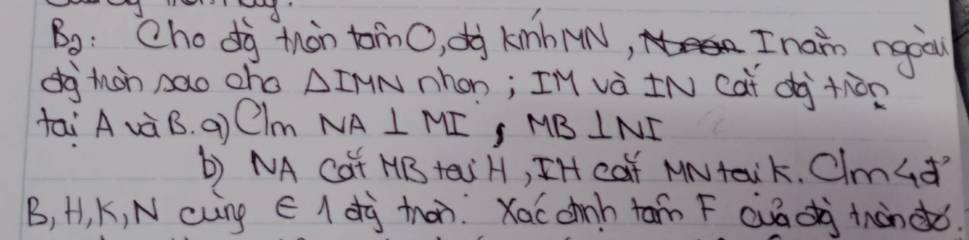
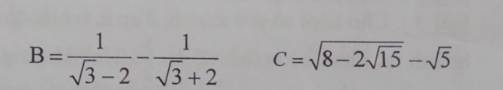

 giúp mik với ạ chỉ cần rút gọn 6 cái biểu thức thui ạ .mong mn giúp đỡ.
giúp mik với ạ chỉ cần rút gọn 6 cái biểu thức thui ạ .mong mn giúp đỡ.