B2:
a) \(\dfrac{1}{x+2}+\dfrac{1}{\left(x+2\right)\left(4x+7\right)}\left(ĐK:x\ne-2;x\ne-\dfrac{7}{4}\right)\)
\(=\dfrac{4x+7}{\left(x+2\right)\left(4x+7\right)}+\dfrac{1}{\left(x+2\right)\left(4x+7\right)}\)
\(=\dfrac{4x+7+1}{\left(x+2\right)\left(4x+7\right)}\)
\(=\dfrac{4x+8}{\left(x+2\right)\left(4x+7\right)}\)
\(=\dfrac{4\left(x+2\right)}{\left(x+2\right)\left(4x+7\right)}\)
\(=\dfrac{4}{4x+7}\)
b) \(\dfrac{3x+5}{x^2-5x}-\dfrac{x-25}{25-5x}\left(ĐK:x\ne0;x\ne5\right)\)
\(=\dfrac{3x+5}{x\left(x-5\right)}+\dfrac{x-25}{5x-25}\)
\(=\dfrac{3x+5}{x\left(x-5\right)}+\dfrac{x-25}{5\left(x-5\right)}\)
\(=\dfrac{5\left(3x+5\right)}{5x\left(x-5\right)}+\dfrac{x\left(x-25\right)}{5x\left(x-5\right)}\)
\(=\dfrac{15x+25+x^2-25x}{5x\left(x-5\right)}\)
\(=\dfrac{x^2-10x+25}{5x\left(x-5\right)}\)
\(=\dfrac{x^2-2\cdot x\cdot5+5^2}{5x\left(x-5\right)}\)
\(=\dfrac{\left(x-5\right)^2}{5x\left(x-5\right)}\)
\(=\dfrac{x-5}{5x}\)
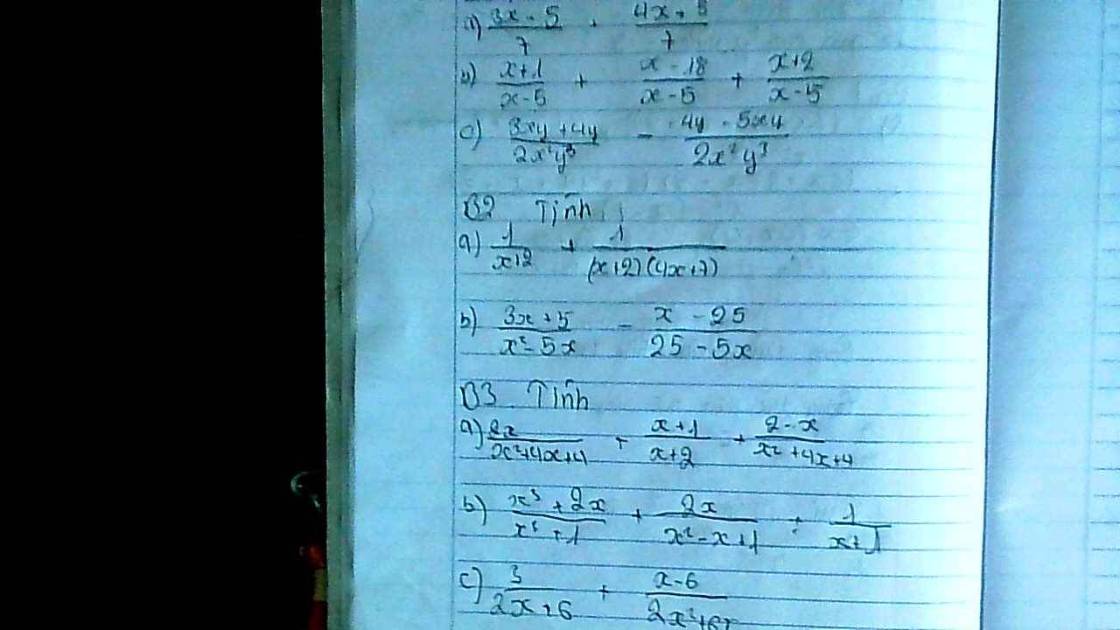
vẽ hình giúp mik nha mik cảm ơn rất rất nhiều
giúp mik câu 5-8 ạ mik cám ơn các bạn, mong mn giúp đỡ vì nay mik thi r, gvbm mới cho đề hồi hôm qua ạ ,mik khá là sốc gvbm có thể kì thị lớp mik như vậy ạ
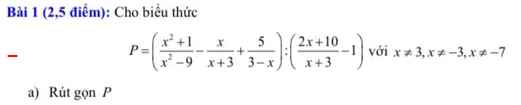
Mn giúp em bài 3 câu bc với em tính số xấu quá, mong mn giúp ạ:(