4)
a)\(4x-5=3\left(x-2\right)\)
⇔\(4x-5=3x-6\)
⇔\(4x-3x=-6+5\)
⇔\(x=-1\)
Vập phương trình có nghiệm là \(x=-1\)
b)\(4x\left(3x-7\right)+5\left(7-3x\right)=0\)
⇔\(12x^2-28x+35-15x=0\)
⇔\(12x^2-48x=0\)
⇔\(12x\left(x-4\right)=0\)
⇔\(12x=0\) hoặc \(x-4=0\)
⇔\(x=0\) hoặc \(x=4\)
Vập phương trình có tập nghiệm là \(S=\left\{0;4\right\}\)
c)\(\dfrac{2x-3}{5}-\dfrac{4x+1}{3}=\dfrac{2x-3}{2}\)
⇔\(\dfrac{6\left(2x-3\right)}{5.6}-\dfrac{10\left(4x+1\right)}{3.10}=\dfrac{15.\left(2x-3\right)}{2.15}\)
⇒\(12x-18-40x-10=30x-45\)
⇔\(12x-40-30=-45+18+10\)
⇔\(-58x=-17\)
⇔\(x=\dfrac{17}{58}\)
Vập phương trình có nghiệm là \(x=\dfrac{17}{58}\)
d)\(\dfrac{x}{x-2}+\dfrac{3}{x+2}=\dfrac{x^2}{x^2-4}\)
\(ĐKXĐ:\left[{}\begin{matrix}x-2\ne0\\x+2\ne0\end{matrix}\right.\Leftrightarrow x\ne\mp2\)
\(\dfrac{x}{x-2}+\dfrac{3}{x+2}=\dfrac{x^2}{x^2-4}\)
⇔\(\dfrac{x\left(x+2\right)}{\left(x-1\right)\left(x+2\right)}+\dfrac{3\left(x-2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{x^2}{\left(x+2\right)\left(x-2\right)}\)
⇒\(x^2+2x+3x-6=x^2\)
⇔\(x^2-x^2+2x+3x=6\)
⇔\(5x=6\)
⇔\(x=\dfrac{6}{5}\)
Vập phương trình có nghiệm là \(x=\dfrac{6}{5}\)
5)
a)\(3x-7\le4\left(2x-3\right)+5\)
⇔\(3x-7\le8x-12+5\)
⇔\(3x-8x\le-12+5+7\)
⇔\(-5x\le0\)
⇔\(-5x.\dfrac{-1}{5}\ge0.\dfrac{-1}{5}\)
⇔\(x\ge0\)
Vậy tập nghiệm của bất phương trình là: \(S=\left\{xIx\ge0\right\}\)
Biểu diễn tập tập nghiệm trên trục số:
b)\(\dfrac{6x-1}{4}-\dfrac{3x-1}{2}>x+\dfrac{7}{3}\)
⇔\(\dfrac{\left(6x-1\right)3}{4.3}-\dfrac{\left(3x-1\right)6}{2.6}>\dfrac{x12}{1.12}+\dfrac{7.4}{3.4}\)
⇒\(18x-3-18x+6>12x+28\)
⇔\(18x-18x-12x>28+3-6\)
⇔\(-12x>25\)
⇔\(-12x\dfrac{-1}{12}< 25\dfrac{-1}{12}\)
⇔\(x< -\dfrac{25}{12}\)
Vậy tập nghiệm của bất phương trình là: \(S=\left\{xIx< -\dfrac{25}{12}\right\}\)
Biểu diễn tập tập nghiệm trên trục số:

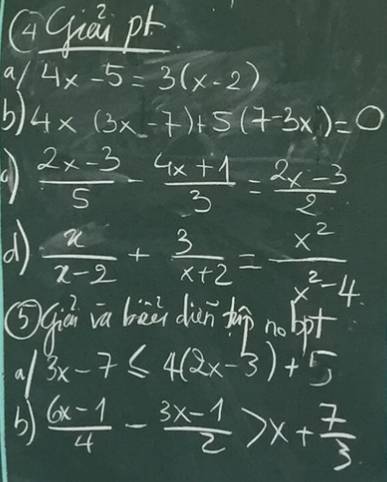 mong các bạn giúp mình cảm ơn
mong các bạn giúp mình cảm ơn











