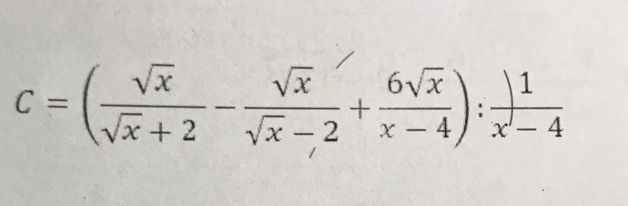2: a: Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}\)
=>\(\dfrac{AB}{10}=sin30=\dfrac{1}{2}\)
=>\(AB=\dfrac{10}{2}=5\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{10^2-5^2}=5\sqrt{3}\left(cm\right)\)
b: Vì BM và BN là hai tia phân giác của hai góc kề bù
nên BM\(\perp\)BN
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-30^0=60^0\)
BM là phân giác của góc ABC
=>\(\widehat{ABM}=\widehat{CBM}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)
ΔMAB vuông tại M
=>\(\widehat{MAB}+\widehat{MBA}=90^0\)
=>\(\widehat{MAB}=90^0-30^0=60^0\)
ΔMAN vuông tại A
=>\(\widehat{AMN}+\widehat{ANM}=90^0\)
=>\(\widehat{ANM}=30^0\)
AMBN là hình chữ nhật(Do có 3 góc vuông)
=>\(\widehat{ANM}=\widehat{BMN}\)
=>\(\widehat{BMN}=30^0\)
Ta có: \(\widehat{BMN}=\widehat{MBC}\left(=30^0\right)\)
mà hai góc này là hai góc so le trong
nên MN//BC
1: Xét ΔBHA vuông tại H có \(cosA=\dfrac{AH}{AB}=\dfrac{20}{60}=\dfrac{1}{3}\)
nên \(\widehat{A}\simeq71^0\)
=>\(\alpha\simeq71^0\)










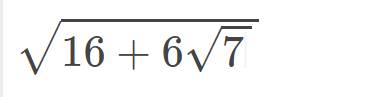 mọi người giúp mình câu này với ạ
mọi người giúp mình câu này với ạ