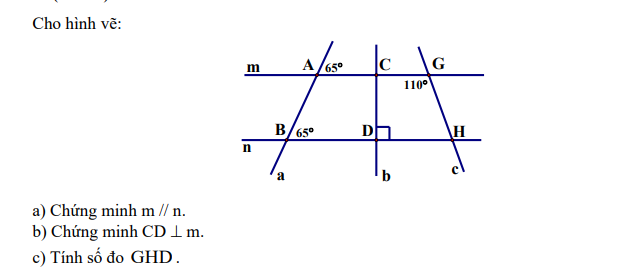
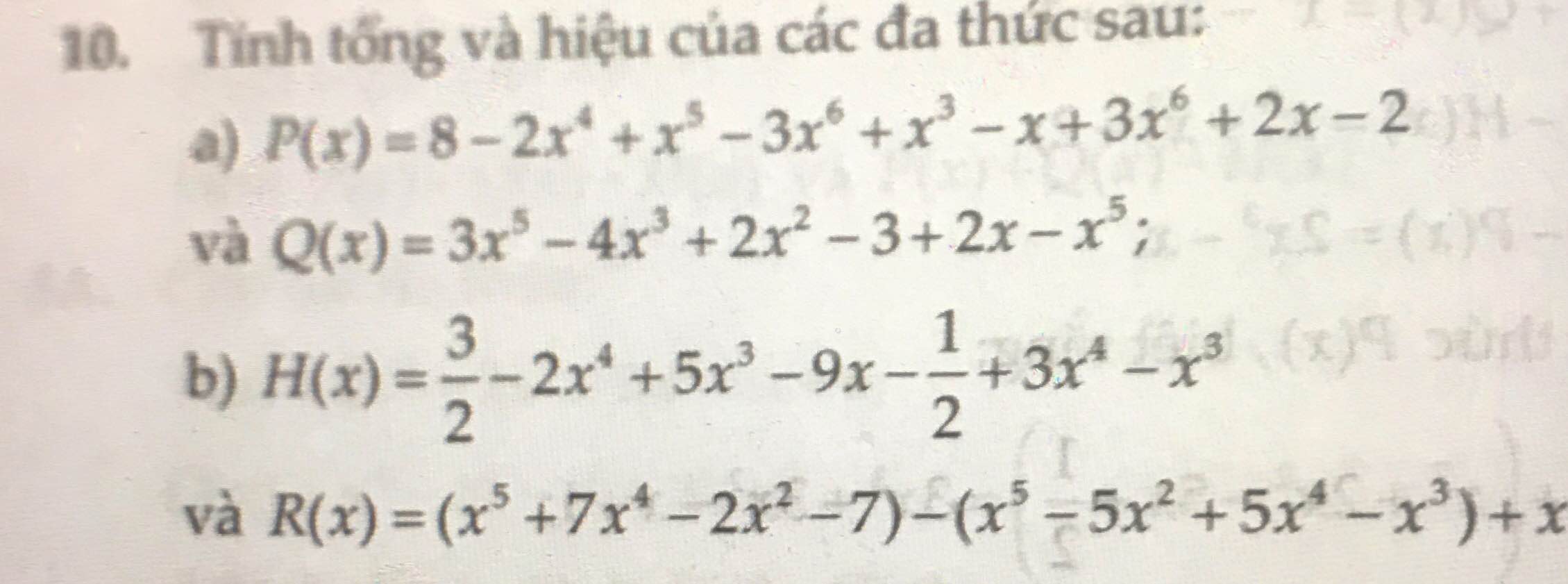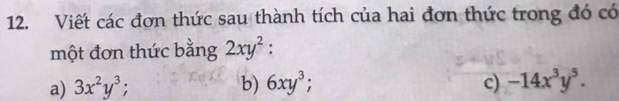Bài 4:
a: Ta có: \(\widehat{ACD}=180^0-\widehat{BAC}\)
=>\(\widehat{ACD}+\widehat{BAC}=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên AB//CD
b: Vẽ Cx là tia đối của tia CD
=>\(\widehat{xCA}+\widehat{ACD}=180^0\)(hai góc kề bù)
=>\(\widehat{xCA}=\widehat{BAC}\)
Ta có: \(\widehat{ACE}=\widehat{xCA}+\widehat{xCE}\)
mà \(\widehat{ACE}=\widehat{BAC}+\widehat{CEF}\)
nên \(\widehat{xCA}+\widehat{xCE}=\widehat{BAC}+\widehat{CEF}\)
mà \(\widehat{xCA}=\widehat{BAC}\)
nên \(\widehat{xCE}=\widehat{CEF}\)
mà hai góc này là hai góc ở vị trí so le trong
nên Cx//EF
=>CD//EF
Bài 3:
a: Ta có: CD\(\perp\)CE
FE\(\perp\)CE
Do đó: CD//FE
b: Kẻ Cx là tia đối của tia CD
Ta có: AB//CD
=>\(\widehat{ACD}+\widehat{CAB}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{ACD}+40^0=180^0\)
=>\(\widehat{ACD}=140^0\)
Ta có: \(\widehat{xCA}+\widehat{DCA}=180^0\)(hai góc kề bù)
=>\(\widehat{xCA}+140^0=180^0\)
=>\(\widehat{xCA}=40^0\)
\(\widehat{ACE}=\widehat{xCA}+\widehat{xCE}=40^0+90^0=130^0\)







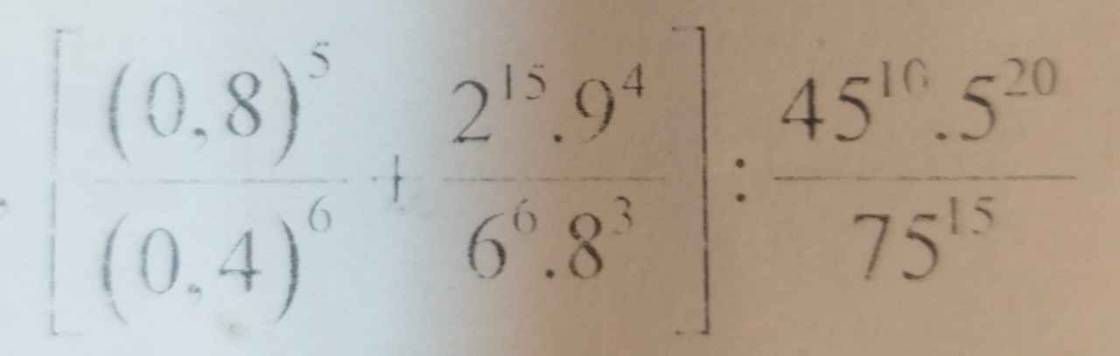






 m
m