a: ΔOCD cân tại O
mà OH là đường cao
nên OH là phân giác của góc COD
Xét ΔOCF và ΔODF có
OC=OD
\(\hat{COF}=\hat{DOF}\)
OF chung
Do đó: ΔOCF=ΔODF
=>\(\hat{OCF}=\hat{ODF}\)
=>\(\hat{ODF}=90^0\)
=>FD là tiếp tuyến của (O)
b: Ta có: \(\hat{FCB}+\hat{OCB}=\hat{OCF}=90^0\)
\(\hat{HCB}+\hat{OBC}=90^0\) (ΔHCB vuông tại H)
mà \(\hat{OCB}=\hat{OBC}\) (ΔOBC cân tại O)
nên \(\hat{FCB}=\hat{HCB}\)
=>CB là phân giác của góc HCF
Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
=>CA⊥CB
=>CA là phân giác ngoài tại đỉnh C của ΔHCF
Xét ΔHCF có CB là phân giác
nên \(\frac{BH}{BF}=\frac{CH}{CF}\)
Xét ΔCHF có CA là phân giác
nên \(\frac{AH}{AF}=\frac{CH}{CF}\)
=>\(\frac{AH}{AF}=\frac{BH}{BF}\)
=>\(AH\cdot BF=AF\cdot BH\)










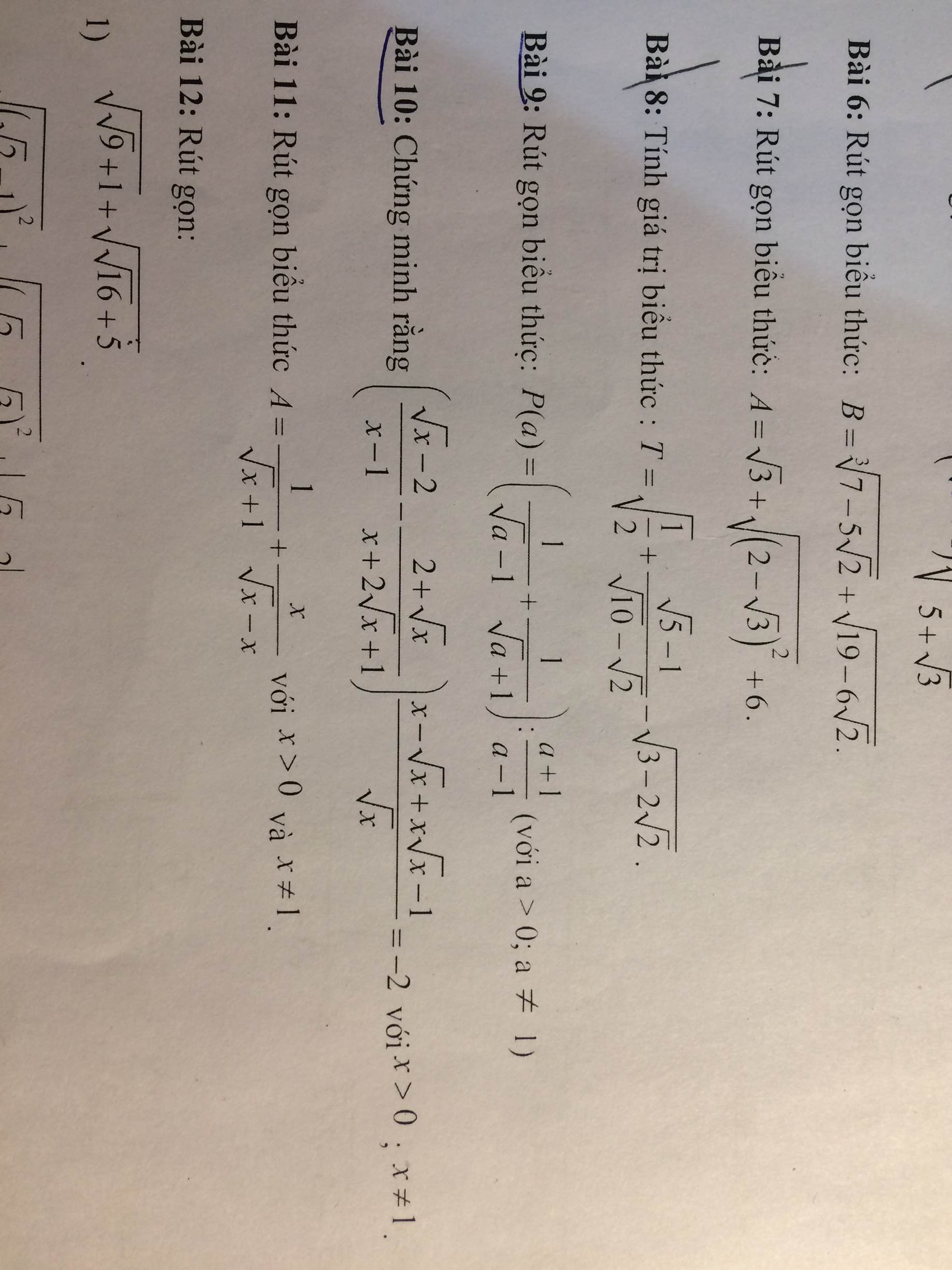







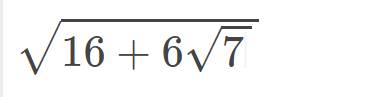 mọi người giúp mình câu này với ạ
mọi người giúp mình câu này với ạ





