1: Xét ΔAHB vuông tại H có \(tanABH=\dfrac{AH}{HB}\)
=>\(BH=\dfrac{45}{tan36}\simeq61,9\left(mét\right)\)
2:
1: Xét ΔABH vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(3\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(4\right)\)
Từ (3),(4) suy ra \(AD\cdot AB=AE\cdot AC\)
Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
nên ADHE là hình chữ nhật
2: Xét ΔABC vuông tại A có AH là đường cao
nên \(AB^2=BH\cdot BC\)(1)
Xét ΔABG vuông tại A có AK là đường cao
nên \(BK\cdot BG=BA^2\left(2\right)\)
Từ (1),(2) suy ra \(BH\cdot BC=BK\cdot BG\)
=>\(\dfrac{BH}{BG}=\dfrac{BK}{BC}\)
Xét ΔBHK và ΔBGC có
\(\dfrac{BH}{BG}=\dfrac{BK}{BC}\)
\(\widehat{HBK}\) chung
Do đó: ΔBHK~ΔBGC
=>\(\dfrac{HK}{GC}=\dfrac{BH}{BG}\)
Xét ΔABC vuông tại A có \(cosABC=\dfrac{AB}{BC}\)
Xét ΔABG vuông tại A có \(sinAGB=\dfrac{AB}{GB}\)
\(sinAGB\cdot cosABC=\dfrac{AB}{BG}\cdot\dfrac{AB}{BC}=\dfrac{AB^2}{BC}\cdot\dfrac{1}{BG}=\dfrac{BH}{BG}=\dfrac{HK}{CG}\)










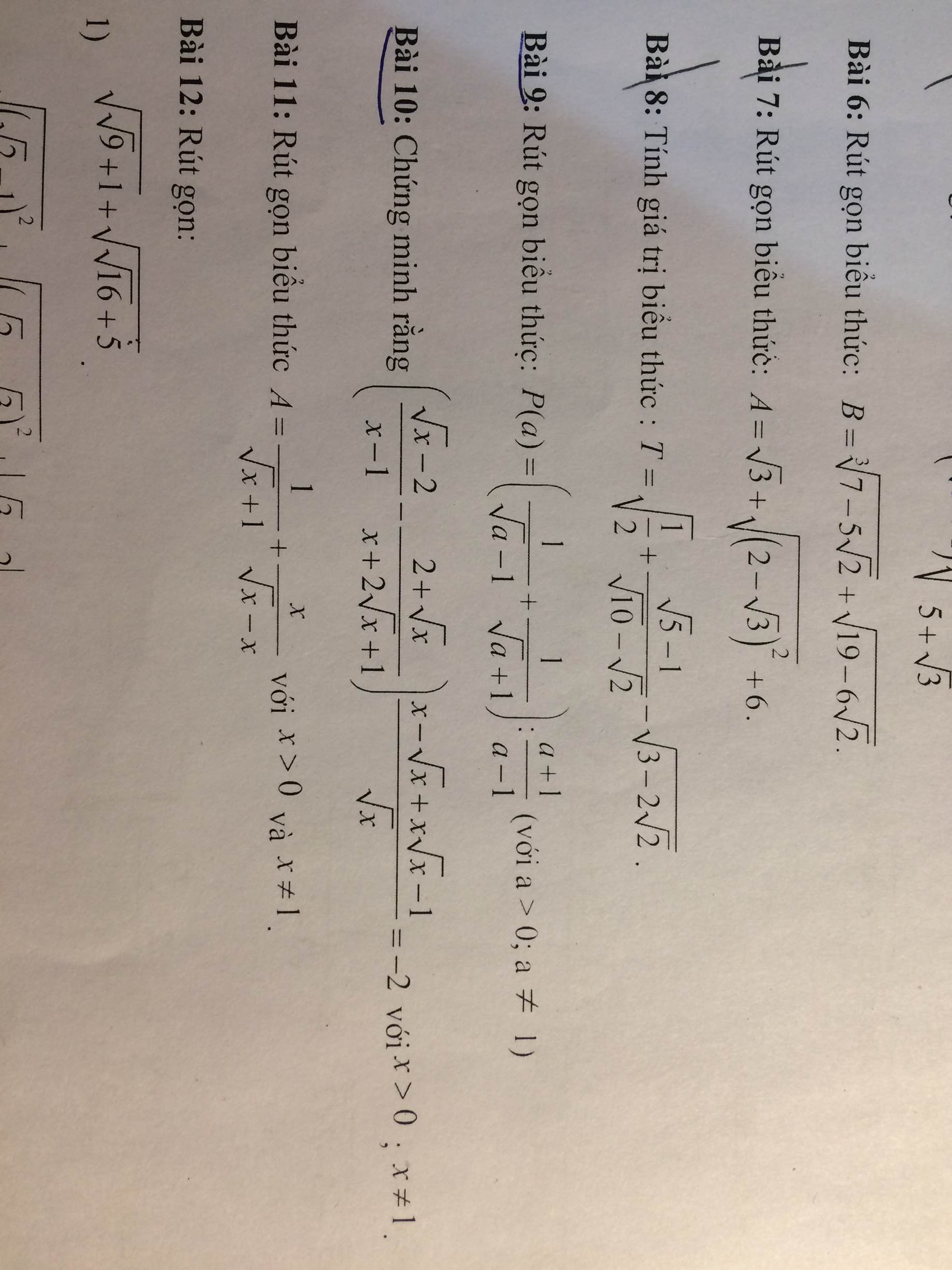







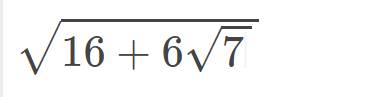 mọi người giúp mình câu này với ạ
mọi người giúp mình câu này với ạ





