Áp dụng bất đẳng thức Cauchy-Schwarz:
\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{3^2}{a+b+c}=\dfrac{9}{3}=3\)
\(\Rightarrow5\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge5.3=15\left(1\right)\)
Áp dụng bất đẳng thức lũy thừa bậc \(8\), ta có:
\(\dfrac{a^8+b^8+c^8}{3}\ge\left(\dfrac{a+b+c}{3}\right)^8=\left(\dfrac{3}{3}\right)^8=1\)
\(\Rightarrow a^8+b^8+c^8\ge3\left(2\right)\)
\(\left(1\right);\left(2\right)\Rightarrow a^8+b^8+c^8+5\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge3+15=18\left(đpcm\right)\)














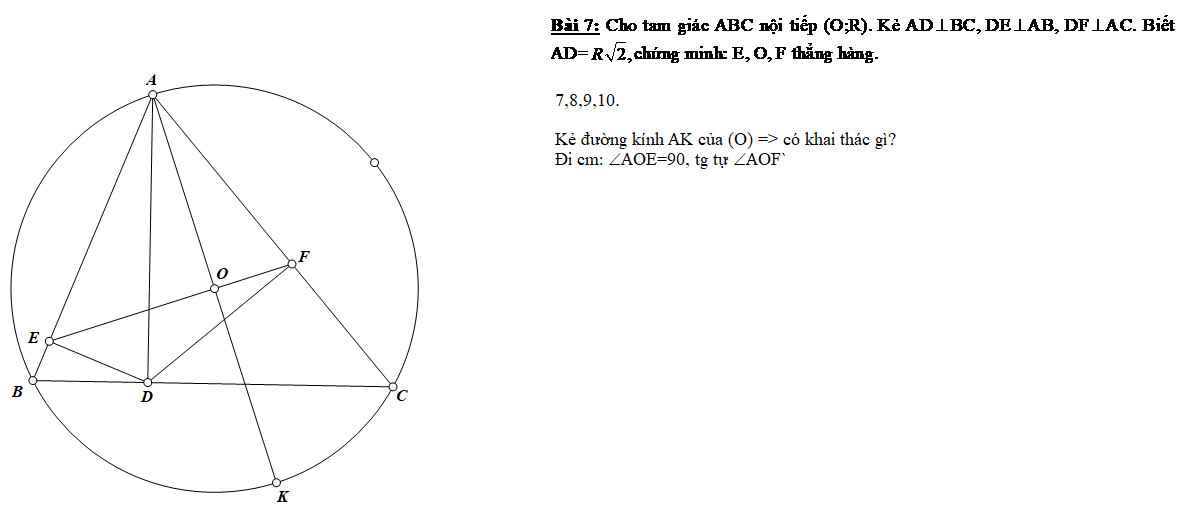



 em cần giải gấp bài 2 ạ, mọi người giúp em với ạ
em cần giải gấp bài 2 ạ, mọi người giúp em với ạ




